Для лучшего уяснения сущности задач поиска и оптимизации проектных решений целесообразно дать геометрическую интерпретацию этих задач. Можно рассмотреть в качестве критерия оптимальности функцию двух переменных – уравнение эллиптического параболоида

Q = x₁²/2p + x₂²/2q, p > 0, q > 0 (1)

Для конкретности можно взять р = 1,5 ; q = 2,5 , тогда функция цели

Q = x₁²/3 + x₂²/5 (2)

Ограничения на изменения параметров следующие:

2x₁ + x₂ ≤ 2.0;
x₁ ≥ -0.5;
x₂ ≥ -1.0.

Они выделяют на плоскости x₁, x₂ область допустимых значений параметров S, показанную на рис.1.

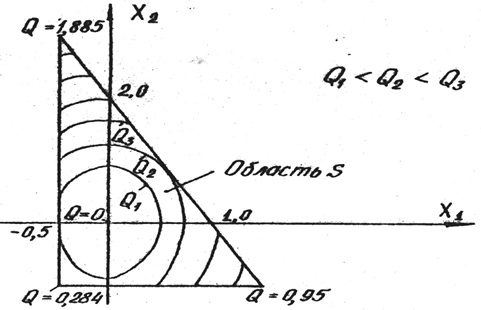
Рис.1. Геометрическое представление задач оптимизации

Плоскости Q = Q_i = const > 0, параллельные плоскости x₁, x₂, пересекают параболоид (1) [(2)] по эллипсам

Q_i = x₁²/2p + x₂²/2q (3)

и образуют так называемые линии равного уровня (рис.1).

В представленном примере функция цели в области допустимых значений параметров имеет один глобальный минимум Q = 0 при x₁ = x₂ = 0 и несколько локальных максимумов, один из которых Q = 1,88 ( x₁ = – 0,5 и x₂ = 3,0 ) является глобальным. Наличие ограничений позволяет говорить только об условных максимумах и минимумах в пределах области S.

Распространяя рассмотренный двумерный пример на более общий случай, можно говорить о том, что ограничения, выделяют область S в n-мерном пространстве параметров x₁, x₂, … , x_n,.

Любая точка в этой области определяет допустимый вариант проекта, который, в свою очередь, характеризуется некоторым значением функции цели.

Подход к решению задач поиска и оптимизации проектных решений во многом определяется особенностями математического описания объектов проектирования, совокупности накладываемых ограничений, поведения функции цели в области допустимых значений параметров. Поэтому необходимо рассмотреть особенности ЭМУС как объектов поиска в оптимизации проектных решений.

Комментарии запрещены.