Различают вероятностные (математические) и статистические показатели надежности. Математические показатели надежности выводятся из теоретических функций распределения вероятностей отказов. Статистические показатели надежности определяются опытным путем при испытаниях объектов на базе статистических данных эксплуатации оборудования.

Надежность является функцией многих факторов, большинство из которых случайны. Отсюда ясно, что для оценки надежности объекта необходимо большое количество критериев.

Критерий надежности – это признак, по которому оценивается надежность объекта.

Критерии и характеристики надежности носят вероятностный характер, поскольку факторы, влияющие на объект, носят случайный характер и требуют статистической оценки.

Количественными характеристиками надежности могут быть:
• вероятность безотказной работы;
• среднее время безотказной работы;
• интенсивность отказов;
• частота отказов;
• различные коэффициенты надежности.

1. Вероятность безотказной работы

Служит одним из основных показателей при расчетах на надежность.
Вероятность безотказной работы объекта называется вероятность того, что он будет сохранять свои параметры в заданных пределах в течение определенного промежутка времени при определенных условиях эксплуатации.

В дальнейшем полагаем, что эксплуатация объекта происходит непрерывно, продолжительность эксплуатации объекта выражена в единицах времени t и эксплуатация начата в момент времени t=0.
Обозначим P(t) вероятность безотказной работы объекта на отрезке времени [0,t]. Вероятность, рассматриваемую как функцию верхней границы отрезка времени, называют также функцией надежности.
Вероятностная оценка: P(t) = 1 – Q(t), где Q(t) — вероятность отказа.

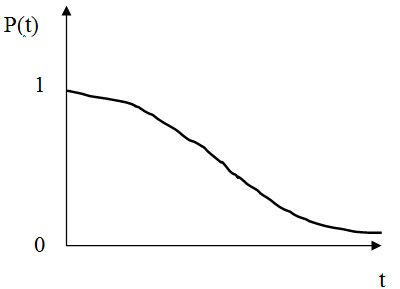
Типичная кривая вероятности безотказной работы

Из графика очевидно, что:
1. P(t) – невозрастающая функция времени;
2. 0 ≤ P(t) ≤ 1;
3. P(0)=1; P(∞)=0.

На практике иногда более удобной характеристикой является вероятность неисправной работы объекта или вероятность отказа:
Q(t) = 1 – P(t).
Статистическая характеристика вероятности отказов: Q*(t) = n(t)/N

2. Частота отказов

Частотой отказов называется отношение числа отказавших объектов к их общему числу перед началом испытания при условии что отказавшие объекты не ремонтируются и не заменяются новыми, т.е

a*(t) = n(t)/(NΔt)
где a*(t) — частота отказов;
n(t) – число отказавших объектов в интервале времени от t – t/2 до t+ t/2;
Δt – интервал времени;
N – число объектов, участвующих в испытании.

Частота отказов есть плотность распределения времени работы изделия до его отказа. Вероятностное определение частоты отказов a(t) = -P(t) или a(t) = Q(t).

Таким образом, между частотой отказов, вероятностью безотказной работы и вероятностью отказов при любом законе распределения времени отказов существует однозначная зависимость: Q(t) = ∫ a(t)dt.

Отказ трактуют в теории надежности как случайное событие. В основе теории лежит статистическое истолкование вероятности. Элементы и образованные из них системы рассматривают как массовые объекты, принадлежащие одной генеральной совокупности и работающие в статистически однородных условиях. Когда говорят об объекте, то в сущности имеют в виду наугад взятый объект из генеральной совокупности, представительную выборку из этой совокупности, а часто и всю генеральную совокупность.

Для массовых объектов статистическую оценку вероятности безотказной работы P(t) можно получить, обработав результаты испытаний на надежность достаточно больших выборок. Способ вычисления оценки зависит от плана испытаний.

Пусть испытания выборки из N объектов проведены без замен и восстановлений до отказа последнего объекта. Обозначим продолжительности времени до отказа каждого из объектов t₁, …, t_N. Тогда статистическая оценка:

P*(t) = 1 — 1/N ∑η(t-t_k)

где η — единичная функция Хевисайда.

Для вероятности безотказной работы на определенном отрезке [0, t] удобна оценка P*(t) = [N — n(t)]/N,
где n(t) – число объектов, отказавших к моменту времени t.

Частота отказов, определяемая при условии замены отказавших изделий исправными, иногда называется средней частотой отказов и обозначается ω(t).

3. Интенсивность отказов

Интенсивностью отказов λ(t) называется отношение числа отказавших объектов в единицу времени к среднему числу объектов, работающих в данный отрезок времени, при условии, что отказавшие объекты не восстанавливаются и не заменяются исправными: λ(t) = n(t)/[N_срΔt]
где N_ср = [N_i + N_i+1]/2 — среднее число объектов, исправно работавших в интервале времени Δt;
N_i – число изделий, работавших в начале интервала Δt;
N_i+1 – число объектов, исправно работавших в конце интервала времени Δt.

Ресурсные испытания и наблюдения над большими выборками объектов показывают, что в большинстве случаев интенсивность отказов изменяется во времени немонотонно.

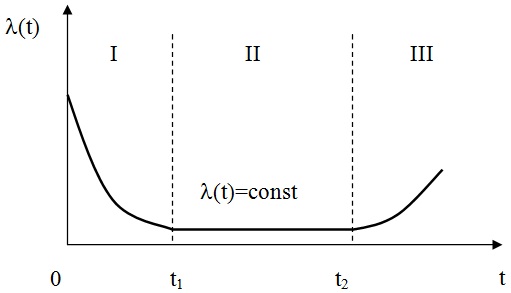
Типичная кривая изменения интенсивности отказов объекта

Из кривой зависимости отказов от времени видно, что весь период работы объекта можно условно поделить на 3 периода.
I — й период – приработка.

Приработочные отказы являются, как правило, результатом наличия у объекта дефектов и дефектных элементов, надежность которых значительно ниже требуемого уровня. При увеличении числа элементов в изделии даже при самом строгом контроле не удается полностью исключить возможность попадания в сборку элементов, имеющих те или иные скрытые дефекты. Кроме того, к отказам в этот период могут приводить и ошибки при сборке и монтаже, а также недостаточная освоенность объекта обслуживающим персоналом.

Физическая природа таких отказов носит случайный характер и отличается от внезапных отказов нормального периода эксплуатации тем, что здесь отказы могут иметь место не при повышенных, а и при незначительных нагрузках («выжигание дефектных элементов»).
Снижение величины интенсивности отказов объекта в целом, при постоянном значении этого параметра для каждого из элементов в отдельности, как раз и объясняется «выжиганием» слабых звеньев и их заменой наиболее надежными. Чем круче кривая на этом участке, тем лучше: меньше дефектных элементов останется в изделии за короткий срок.

Чтобы повысить надежность объекта, учитывая возможность приработочных отказов, нужно:
• проводить более строгую отбраковку элементов;
• проводить испытания объекта на режимах близких к эксплуатационным и использовать при сборке только элементы, прошедшие испытания;
• повысить качество сборки и монтажа.

Среднее время приработки определяют при испытаниях. Для особо важных случаев необходимо увеличить срок приработки в несколько раз по сравнению со средним.

II — й период – нормальная эксплуатация
Этот период характеризуется тем, что приработочные отказы уже закончились, а отказы, связанные с износом, еще не наступили. Этот период характеризуется исключительно внезапными отказами нормальных элементов, наработка на отказ которых очень велика.

Сохранение уровня интенсивности отказов на этом этапе характеризуется тем, что отказавший элемент заменяется таким же, с той же вероятностью отказа, а не лучшим, как это происходило на этапе приработки.

Отбраковка и предварительная обкатка элементов, идущих на замену отказавших, имеет для этого этапа еще большее значение.
Наибольшими возможностями в решении этой задачи обладает конструктор. Нередко изменение конструкции или облегчение режимов работы всего одного-двух элементов обеспечивает резкое повышение надежности всего объекта. Второй путь – повышение качества производства и даже чистоты производства и эксплуатации.

III – й период – износ
Период нормальной эксплуатации заканчивается, когда начинают возникать износовые отказы. Наступает третий период в жизни изделия – период износа.

Вероятность возникновения отказов из-за износов с приближением к сроку службы возрастает.

С вероятностной точки зрения отказ системы в данном промежутке времени Δt = t₂ – t₁ определяется как вероятность отказа:

∫a(t) = Q₂(t) — Q₁(t)

Интенсивность отказов есть условная вероятность того, что в промежуток времени Δt произойдет отказ при условии, что до этого он не произошел λ(t) = [Q₂ — Q₁]/[ΔtP(t)]
λ(t) = lim [Q₂ — Q₁]/[ΔtP(t)] = [dQ(t)]/[P(t)dt] = Q'(t)/P(t) = -P'(t)/P(t)
так как a(t) = -P'(t), то λ(t) = a(t)/P(t).

Эти выражения устанавливают зависимость между вероятностью безотказной работы, частотой и интенсивностью отказов. Если a(t) – невозрастающая функция, то справедливо соотношение:
ω(t) ≥ λ(t) ≥ a(t).

4. Среднее время безотказной работы

Средним временем безотказной работы называется математическое ожидание времени безотказной работы.

Вероятностное определение: среднее время безотказной работы равно площади под кривой вероятности безотказной работы.

T = ∫P(t)dt

Статистическое определение: T* = ∑θ_i/N₀
где θ_I – время работы i-го объекта до отказа;
N₀ – начальное число объектов.

Очевидно, что параметр Т* не может полностью и удовлетворительно характеризовать надежность систем длительного пользования, так как является характеристикой надежности только до первого отказа. Поэтому надежность систем длительного использования характеризуют средним временем между двумя соседними отказами или наработкой на отказ t_ср:
t_ср = ∑θ_i/n = 1/ω(t),
где n – число отказов за время t;
θ_i – время работы объекта между (i-1)-м и i-м отказами.

Наработка на отказ – среднее значение времени между соседними отказами при условии восстановления отказавшего элемента.

Комментарии запрещены.