Рассмотрены цифровые алгоритмы спектрального и кепстрального анализа, а также цифрового преобразования Гильберта, используемые при обработке сигналов компьютерными электронными процессорами в лазерной доплеровской анемометрии и виброметрии потоков жидкости и газа. Приведены результаты анализа погрешностей оценки скорости, амплитуды виброколебаний, размера и концентрации рассеивающих частиц в потоке.

Введение

При экспериментальных исследованиях характеристик потоков жидкостей и газов широкое распространение получили бесконтактные и не возмущающие исследуемую среду оптические методы. Измерение скоростей поступательного либо колебательного движения частиц в таких потоках в настоящее время с хорошей пространственно-временной локализацией проводится при помощи лазерных доплеровских анемометров (ЛДА) и виброметров (ЛДВ). Они представляют собой сложные измерительные системы, состоящие из лазера, оптико-механического блока, фотоприемника, электронного процессора обработки сигналов и программного обеспечения. Информацию о среднем за малый интервал времени значении локальной скорости потока получают путем анализа излучения, рассеянного движущейся в потоке частицей, при просвечивании исследуемой области когерентными лазерными пучками. В целях повышения точности измерений, обеспечения их автоматизации, а также в целях унификации аппаратных и программных средств на практике все большее распространение получают компьютерные измерительные системы (КИС).

В ЛДА и ЛДВ такого типа сигналы, содержащие измерительную информацию и поступающие с выхода оптического датчика, вводятся при помощи высокопроизводительного стандартного интерфейса в компьютер, где обрабатываются с использованием специализированных цифровых алгоритмов. Использование микроЭВМ как составной части цифрового электронного процессора обработки сигнала позволяет реализовать сложные алгоритмы обработки и их адаптацию к принимаемому сигналу, характерные для интеллектуальных измерительных систем.

Применение дополнительных аппаратных средств в виде цифровых сигнальных процессоров дает возможность во многих случаях проводить анализ поступающих сигналов в реальном масштабе времени. В настоящее время за рубежом серийно выпускаются несколько типов электронных процессоров, специально разработанных для анализа доплеровских сигналов и использующих идеологию КИС. В частности, известны варианты счетно-импульсных систем (IFA 550 фирмы TSI,США), системы с адаптивной автокорреляционной обработкой (IFA 750 фирмы TSI, США), процессоры, использующие периодограммный метод анализа доплеровских сигналов (импульсный цифровой спектральный анализатор BSA фирмы Dantec, Дания) и другие. Однако, возможности используемых в процессорах данного типа методов анализа и их погрешности до сих пор недостаточно изучены. Рассмотрим результаты анализа ряда цифровых алгоритмов, которые могут быть использованы для обработки сигналов ЛДА и ЛДВ компьютерными электронными процессорами.

Спектральный метод анализа

Одним из наиболее распространенных в настоящее время методов анализа доплеровских сигналов является спектральный метод. С его помощью проводится, в частности, измерение доплеровского сдвига частоты сигналов ЛДА. Воспользуемся известной [1] интерференционной моделью дифференциальной схемы анемометра, согласно которой при прохождении рассеивающей частицы через центр измерительного объема, образованного областью пересечения двух когерентных пучков, сигнал на выходе фотоприемника (без учета шума) имеет вид

u(t)=U_m[1+Mcos(Ω_mt±2πv_xt/Λ)]exp{-2(v_xt/w_o)²}, (1)

где U_m — среднее значение сигнала в центре импульса,
M — индекс амплитудной модуляции,
Ω_m — разность частот интерферирующих пучков,
v_x — измеряемая проекция вектора скорости частицы,
Λ — период интерференционной картины,
w_o — эффективный радиус измерительного объема.

Скорость рассеивающей частицы определяется косвенным путем по результатам измерений частоты заполнения радиоимпульса (1)

f_s =|Ω_m/2π± vx/Λ|

а погрешность оценки скорости складывается из погрешностей измерения величин Ω_m, Λ и f_s. При условии, что параметры Ω_m и Λ известны точно, относительная погрешность измерения скорости рассеивающей частицы может быть найдена из выражения

δ_v = δ_f/|1±Ω_m/2πf_s| (2)

Подробный анализ цифровых методов измерения f_s сигнала (1) и оценка их погрешностей проведены в [2-4]. Исходная информация о принятом сигнале содержится в выборке из N отсчетов x_к смеси сигнала и шума, взятых с интервалом T_o. Спектральный алгоритм измерения частоты сигнала ЛДА, проанализированный в [2], использует в качестве оценки f_s координату максимума модуля спектральной плотности импульса (1), пропущенного через схему предварительной фильтрации. При этом спектральная плотность импульса определяется как дискретное преобразование Фурье (ДПФ) выборки, а положение максимума модуля спектральной плотности рассчитывается при помощи гауссовой аппроксимации огибающей дискретного спектра по трем наибольшим отсчетам. Расчетная формула для оценки f_s имеет вид

f^_s = Ω/2π[r₀ — ln(c₁/c₃) / 2ln(c₂²/c₁c₃] (3)

где C₁=|C(r_oΩ-Ω)|, C₂=|C(r_oΩ)|, C₃=|C(r_oΩ+Ω)| — модули коэффициентов ДПФ выборки отсчетов сигнала с номерами r_o-1, r_o и r_o+1 (r_o — номер максимального по модулю отсчета в окрестности частоты f_s), а Ω=2π/(NT_o)интервал дискретизации спектра.

Относительная погрешность измерения частоты f_s содержит систематическую и случайную составляющие. Систематическая составляющая погрешности носит методический характер и обусловлена фильтрацией и дискретизацией сигнала, а также неточностью используемой расчетной формулы (3). Погрешность фильтрации появляется вследствие деформации спектра исследуемого сигнала частотной характеристикой входного полосового фильтра. Причиной возникновения погрешности дискретизации являются искажения спектра дискретного сигнала по сравнению с исходным спектром, приводящие к смещению положения максимума модуля его спектральной плотности. Данные искажения становятся существенными при предельно малых значениях частоты дискретизации, близких к удвоенной верхней граничной частоте спектра сигнала (1). Последняя из составляющих методической погрешности обусловлена неточностью расчетной формулы (3), которая не учитывает влияние низкочастотной части спектра сигнала (1) на координату максимума модуля его спектральной плотности в окрестности частоты f_s.

Источниками возникновения случайной составляющей погрешности оценки доплеровской частоты являются неточность установки частоты дискретизации и погрешность расчета коэффициентов ДПФ выборки. При использовании высокостабильных генераторов опорных колебаний с цифровым контролем частоты выходного гармонического сигнала можно полагать, что случайная составляющая погрешности определяется отношением сигнал-шум на выходе фотоприемника, инструментальной погрешностью электронного блока и размером обрабатываемой выборки.

Алгоритмы цифрового спектрального анализа могут быть с успехом использованы и при решения задач виброметрии. В других статьях рассмотрены различные методы оценки амплитуды виброколебаний с использованием ЛДВ. Показано, что при наличии сдвига частот интерферирующих пучков выходной сигнал ЛДВ представляет собой частотно-модулированное колебание вида

U(t)=U_ocos[Ω_st+2π(L/Λ)sin(Ω_vt+φ)+β], (4)

Амплитуда вибрации определяется из (4) по измеренному значению индекса частотной модуляции m=2π(L/Λ). Значения m при малых значениях амплитуды L<< Λ можно провести спектральным методом, оценивая относительный уровень боковых гармоник спектра сигнала относительно гармоники частоты Ω_s .

Измерительная информация оказывается заключенной в значении одного или нескольких параметров узкополосного сигнала.

Известно, что произвольный узкополосный сигнал может быть представлен в следующем виде:

U(t) = U_о(t)cos[ω_ot + ϕ_s(t)] = U_о(t)cos φ_s(t), (5)

где U_о(t) — огибающая, ω_o— центральная частота, ϕ_s(t) — начальная фаза, а φ_s(t) — полная фаза сигнала, которая определяется соотношением

φ_s(t) = ω_ot + ϕ_s(t)

Функции U_о(t) и ϕ_s(t) являются медленно меняющимися во времени по сравнению с cos ω_ot, в связи с чем сигнал U(t) называют квазигармоническим. Мгновенной частотой сигнала называется при этом скорость изменения его полной фазы, равная

ω_s(t) = dφ_s(t)/dt = ω_o + dϕ_s(t)/dt.

При компьютерной реализации цифровых алгоритмов обработки узкополосных сигналов последние представлены в дискретной форме массивом из N отсчетов своих мгновенных значений {U_к}, где U_к=U(kT_o), k=1,..,N, T_o — интервал дискретизации. Задача восстановления отсчетов огибающей и полной фазы сигнала по заданному массиву отсчетов его мгновенных значений в общем случае не имеет однозначного решения. Одним из способов ликвидации неоднозначности является использование обобщения векторного представления гармонического колебания на случай узкополосных сигналов. Считается, что узкополосному сигналу соответствует вектор (точка на комплексной плоскости) Ý(t) = U(t) + jÙ(t), мнимая часть которого может быть найдена как преобразование Гильберта от исходного сигнала. Длина вектора (модуль комплексной функции Ý(t)) принимается за огибающую сигнала U(t), а угол между вектором и вещественной осью комплексной плоскости (аргумент комплексной функции Z(t)) — за полную фазу сигнала. В этом случае огибающая описывается выражением

U_о(t) = [U²(t) + Ù²(t) ]^1/2,

а полная фаза и мгновенная частота могут быть найдены по формулам:

φ_s(t)= ω_ot + ϕ_s(t)= Arctg[Ù(t)/U(t)],

ω_s(t) = ω_o + dϕ_s(t)/dt = d/dt{Arctg[Ù(t)/U(t)]}.

Вышеприведенные выражения позволяют однозначно восстановить полную фазу и мгновенную частоту узкополосного сигнала по его реализации. В случае цифровой обработки вычисление отсчетов сопряженного по Гильберту сигнала Ù(t) может быть проведено спектральным методом. Вначале с использованием дискретного преобразования Фурье (ДПФ) находится массив отсчетов дискретного спектра исходного сигнала. Спектральная плотность сопряженного сигнала S_u(ω) связана со спектром исходного сигнала S_u(ω) известным соотношением

S_u(ω) = jS_u(ω), ω <0 S_u(ω) = -jS_u(ω), ω >0

Массив отсчетов сопряженного сигнала Ù(t) можно теперь найти при помощи обратного ДПФ. Отсчеты полной фазы φ_s(kT_o) и частоты ω_s(kT_o) сигнала, рассчитанные в соответствии с приведенными выражениями, могут служить оценками мгновенных значений данных параметров. Смещение и дисперсия этих оценок связаны с недостаточной узкополосностью сигнала U(t), наличием аддитивного шума, а также погрешностями за счет цифровой реализации метода. Графики зависимости погрешности оценки среднего значения частоты одночастичного сигнала ЛДА с гауссовой формой огибающей методами цифрового спектрального анализа (ЦСА) и цифрового преобразования Гильберта (ЦПГ) от отношения сигнал-шум в центре импульса q, полученные ранее для двух значений числа отсчетов n на периоде доплеровских колебаний, приведены на рис.1.

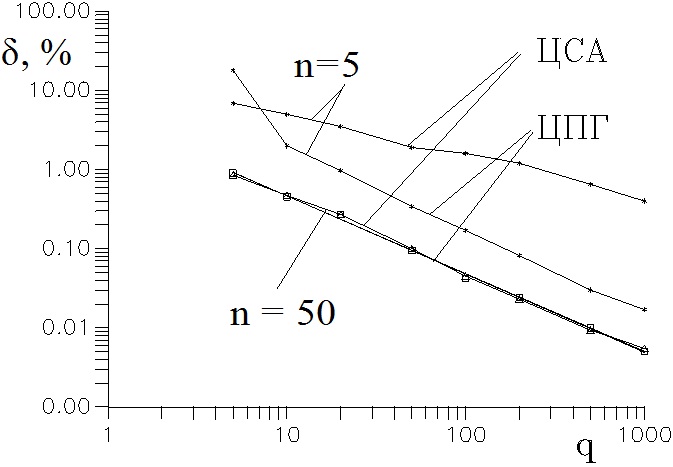
Рис.1 Погрешности оценки среднего значения частоты одночастичного сигнала ЛДА методами ЦСА и ЦПГ

Сравнение графиков показывает, что при малом отношении сигнал-шум более высокую точность измерений обеспечивает метод ЦСА. С другой стороны, достоинством метода ЦПГ является то, что он позволяет получить оценки мгновенных значений частоты сигнала при предельно малом числе отсчетов на периоде доплеровских колебаний. Возможности применения метода ЦПГ для оценки параметров сигналов ЛДВ и погрешности оценки амплитуды виброколебаний были подробно исследованы. С использованием вышерассмотренной модели сигнала (4) было показано, что амплитуда колебаний рассеивающих частиц определяется соотношением

L= (Λ/2π)ΔΩ/Ω_v, (6)

δ_L = δ_Λ + δ_ΔΩ.

Погрешность измерения девиации частоты связана с недостаточной узкополосностью сигнала (4), конечной длительностью интервала наблюдения, ограниченным числом отсчетов в выборке и наличием шума. Графики зависимости случайной составляющей относительной погрешности оценки амплитуды от величины нормированной амплитуды колебаний для различных значений отношения сигнал-шум, полученные методом численного моделирования, приведены на рис.2.

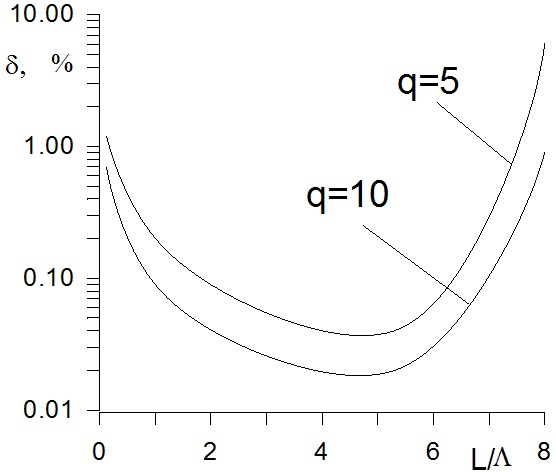
Рис.2 Погрешность оценки амплитуды виброколебаний

Из графиков видно, что погрешность измерений резко возрастает как при увеличении амплитуды колебаний свыше некоторого уровня, так и при ее значительном уменьшении. В первом случае это связано с нарушением узкополосности сигнала, а во втором — с наличием шума, который ограничивает чувствительность метода.

Кепстральный анализ

В одночастичном режиме работы ЛДА при малых размерах рассеивающих частиц сигнал на выходе фотоприемника имеет вид (1). Спектр данного элементарного сигнала состоит из низкочастотной и высокочастотной компонент гауссовой формы. Рассмотрим двухфазный поток с такой концентрацией частиц, при которой появление двух рассеивающих центров в измерительном объеме ЛДА является наиболее вероятным. В этом случае доплеровский сигнал является суммой двух гауссовых радиоимпульсов с той или иной степенью перекрытия. В этом случае спектр доплеровского сигнала оказывается изрезанным, и в нем имеется несколько локальных максимумов. Число таких максимумов и их положение на оси частот зависит от временного интервала между перекрывающимися импульсами. Анализ показывает, что наличие пульсаций спектра сигнала ЛДА в двухчастичном режиме работы анемометра в общем случае может приводить к значительной дополнительной погрешности спектральной оценки доплеровской частоты. Аналогичная ситуация возникает при обработке доплеровских сигналов, рассеянных одиночной частицей больших размеров.

На основании изложенного становится ясно, что при обработке доплеровских сигналов необходимо учитывать сложную структуру их спектра, что позволяет уменьшить погрешность оценки скорости частиц и получить дополнительную информацию об их размерах или концентрации. Одним из методов восстановления спектра одиночного импульса и оценки временного интервала между импульсами является кепстральный анализ, предложенный впервые как эвристический метод определения моментов прихода отражений составного сигнала. Возможности данной методики для оценки параметров сигналов ЛДА были исследованы ранее методом численного моделирования. Компьютерная модель учитывала параметры оптической схемы анемометра, количество частиц в измерительном объеме ЛДА, их размеры и траектории движения. Цифровая кепстральная обработка была использована для уменьшения погрешности оценки скорости путем восстановления спектра элементарного доплеровского сигнала, а также для определения режима работы ЛДА, размеров частиц и расстояния между ними. Алгоритм обработки предусматривал предварительную фильтрацию сигнала и расчет кепстров его высокочастотной и низкочастотной составляющих. При наличии пиков в кепстре низкочастотной составляющей делался вывод о том, что сигнал является откликом от нескольких частиц или от одной, пролетающей вблизи границ измерительного объема. В случае отсутствия пиков регистрировался одночастичный режим работы ЛДА. Пики в кепстре высокочастотной составляющей наблюдались как при обработке сигналов от нескольких частиц, так и от одной большой частицы. При этом координата первого максимума в кепстре в двухчастичном режиме соответствовала временному интервалу между частицами, а в одночастичном режиме — диаметру частицы.

Проведенные исследования влияния кепстральной обработки на погрешность оценки доплеровской частоты сигнала ЛДА спектральным методом показали, что фильтрация кепстра дает заметные положительные результаты при размерах большой частицы либо расстояниях между малыми частицами более 1.5w₀. При малых уровнях шума (отношение сигнал-шум не менее 20 дБ) погрешность измерений уменьшается за счет кепстральной обработки в 50-100 раз. Осциллограмма и график модуля спектральной плотности двухчастичного сигнала ЛДА приведены на рис.3.

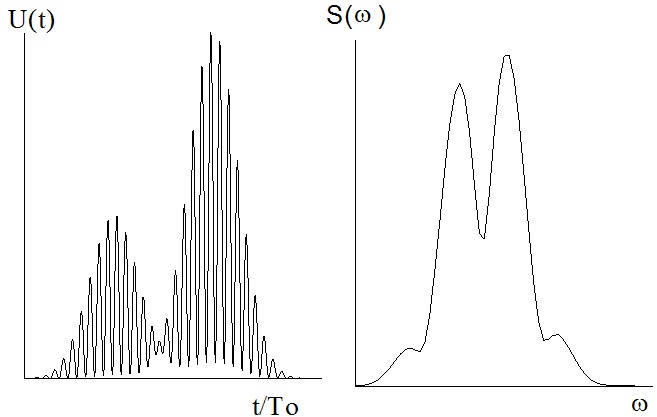
Рис.3 Осциллограмма и спектральная плотность двухчастичного сигнала ЛДА

Цифровой кепстральный анализ использовался также для оценки расстояния между частицами в двухчастичном режиме работы. Численное моделирование показало, что при интервале между частицами менее 1.5w₀ фиксируется одночастичный режим. При расстояниях между частицами более 2w0 погрешность оценки расстояния составляет менее 0,1% при отношении сигнал-шум 40 дБ.

Методом численного моделирования была также исследована зависимость погрешности измерения радиуса r большой частицы от его отношения к радиусу пучка. При r/w₀<0.5-0.7 используемый алгоритм не позволял распознавать большую частицу, либо давал оценку радиуса с большой погрешностью. В случае r/w₀ > 1 погрешность оценки радиуса составляла доли процента.

Заключение

Анализ результатов исследований позволяет сделать вывод, что в настоящее время имеется достаточно широкий набор цифровых алгоритмов, позволяющих проводить обработку сигналов лазерных доплеровских анемометров и виброметров. Представленные алгоритмы обладают повышенной точностью и нашли применение для решения таких задач, как измерение периода интерференционного поля [4], исследование тонкой структуры доплеровского сигнала от большой частицы [10-12], оценка параметров сигнала ЛДВ при изучении акустических колебаний пузырьков газа в жидкости [15].

Литература
1.Ринкевичюс Б.С. Лазерная диагностика потоков / Под ред. В.А.Фабриканта — М.:Изд-во МЭИ. 1990. -288с.
2.Гречихин В.А., Ринкевичюс Б.С. Погрешности цифровых методов измерения частоты одночастичного сигнала ЛДА // Измерительная техника. 1993. N 10. С.43-46.
3.Буренков Ю.А., Гречихин В.А.,Ринкевичюс Б.С. Анализ погрешностей цифровых алгоритмов измерения частоты сигнала ЛДА методом численного моделирования // Измерительная техника. 1995. N 7. С.36-38.
4.Гречихин В.А. Разработка компьютерных алгоритмов обработки одночастичных сигналов лазерных доплеровских анемометров. Дисс….канд. техн. наук. Москва. МЭИ (ТУ).1996 г.
5. Karasik A.Ya., Rinkevichius B.S., Zubov V.A.. Laser Interferometry Principles / Ed. by B.S.Rinkevichius. Mir Publishers and CRC Press, Moscow and Boca Raton. 1995.
6. Дубнищев Ю.Н., Ринкевичюс Б.С. Методы лазерной доплеровской интерферометрии. — Москва. Наука. 1982. -303с.
7. Марпл-мл. С.Л. Цифровой спектральный анализ и его приложения / Пер. с англ. — М.: Мир. 1990. — 584с.
8.Гречихин В.А. Оценка полной фазы узкополосного сигнала с использованием цифрового преобразования Гильберта / Тезисы докл. Международной НТК «Проблемы радиоэлектроники», Москва, 19-21 апреля 1995г.,»Магистр”, 1995, N 2, с.3-4.
9.Grechikhin V.A., Rinkevichius B.S. Digital Hilbert transform for processing of laser Doppler vibrometer signals / In Second Int. Conf. on Vibration Measurements by Laser Techniques: Advances and Applications, E.P.Tomasini, Editor, 1996, Proc. SPIE 2868, p.89 — 96.
10. —
11.Tolkachev A.V. and others. Experimental Research of LDA Signals from a Large Particle // In Laser Anemometry: Advances and Applications. Proc. of the 7th Int. Conf., Karlsruhe. 1997, p.371-378.
12. —
13.D.G.Childers, D.P.Skinner, R.C.Kemerait. The Cepstrum: A Guide to Processing. Proc. IEEE , 1977, Vol.65, N 10, pp.1428-1443.
14. Aleksandrov S.A., Grechikhin V.A., Rinkevichius B.S. The cepstral analysis of LDA signals // In : Modern Techniques and Measurements in Fluid Flows. Proc. 3rd International Conference on Fluid Dynamic Measurement and Its Applications, Beijing, China, 1997, October 14-17, pp.112-114
15. Grechikhin V.A., Rinkevichius B.S., Stepanov A.V., Tolkachev A.V., Greated C.A., Hann D.B.The research on oscillations of gas bubbles in an underwater ultrasonic field. In: Optical Methods in Research of Flows Dinamic. London. 1998, April 16-17, pp.351-363.

Комментарии запрещены.