Рассмотрим непрерывную случайную величину X с функцией распределения F(x), которую предположим непрерывной и дифференцируемой. Вероятность попадания этой случайной величины на участок от х до х+Δх:
F(x < X < x +Δx) = F(x +Δx) - F(x), т.е. приращение функции распределения на этом участке. Рассмотрим отношение этой вероятности к длине участка, т.е. среднюю вероятность, приходящуюся на единицу длины на этом участке, и будем приближать Δх к нулю. В пределе получим производную от функции распределения:

lim _Δx→0 = [F(x + Δx) — F(x)]/Δx = F'(x)

Введем обозначение: f(x) = F'(x).

Функция f(x) называется плотностью распределения («плотностью вероятности») непрерывной величины Х. Функцию f(x) называют дифференциальным законом распределения величины Х.

Плотность распределения, так же как и функция распределения, есть одна из форм закона распределения. Эта форма не является универсальной (в противоположность функции распределения); она существует только для непрерывных величин.

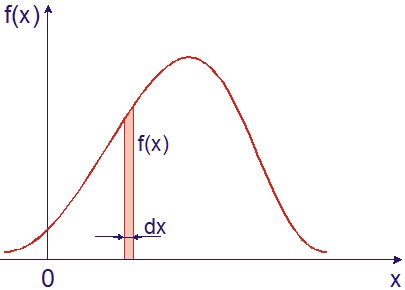
Рассмотрим непрерывную случайную величину Х с плотностью распределения f(x) и элементарный участок dx, примыкающий к точке х. Вероятность попадания случайной величины Х на этот элементарный участок равна f(x) dx. Величина f(x) dx называется элементом вероятности.

Основные свойства плотности распределения:
1. f(x) – неотрицательная функция т.е. f(x) ≥ 0;
2. ∫f(x) dx = 1.

Функция F(x) величина безразмерная. Размерность плотности распределения f(x) обратная размерности случайной величины.

Комментарии запрещены.