Будем предполагать, что минимизируемая функция Q(x) в задаче принадлежит классу K_L функций, удовлетворяющих условию типа условия Липшица с известной константой L:

|Q(x¹) — Q(x²)| ≤ Lρ(x¹, x²), x¹, x²∈D_x, (6.10)

где ρ(x¹, x²) — непрерывная, ограниченная функция, характеризующая расстояние между точками x¹ и х² (например,

ρ(x¹, x²) = ||x¹ — x²||

или

ρ(x¹, x²) = max |x_i¹ — x_i²|.

Рассмотрим вопрос построения для фиксированного числа испытаний N оптимальной пассивной стратегии X_n = (х¹, х², …, х^N), являющейся решением следующей экстремальной задачи:

W(X_N) = min max |Q* — Q(x^k)|, (6.11)

Как было показано в поиске глобального минимума кривой с помощью стохастических автоматов, решение задачи (6.11) сводится к построению оптимального покрытия множества D_x совокупностью r-шаров S (xⁱ, r*) с центрами в точках хⁱ и радиусом r*:

∪S(xⁱ, r*)⊃D_x, (6.12)

В этом случае оптимальная на классе K_L пассивная стратегия Х_N* не зависит от значения константы Липшица L, которая фигурирует только в оценке критерия эффективности алгоритма пассивного поиска:

W(X_N*) = r(X_N*)L. (6.13)

Задача оптимального покрытия прямоугольного параллелепипеда шарами одинакового радиуса (6.12) является нерешенной задачей дискретной геометрии. Поэтому рассмотрим частный случай этой задачи когда область D_x является двумерным координатным квадратом, который покрывается кругами одинакового радиуса.

Для изложения алгоритма построения оптимальной системы узлов X_N* для двумерного квадрата D введем следующие определения.

Функция расстояния ρ(х, хⁱ) между точками х и хⁱ называется нормальной, если область r -шара S (хⁱ, r)⊂D является односвязным множеством для любых r > 0.

Областью Дирихле S(хⁱ) точки хⁱ называется множество точен x∈D таких, что

ρ(х, хⁱ) ≤ ρ(х, х^k), k = 1, 2, …, N, k ≠ i.

Другими словами, область Дирихле точки хⁱ включает точки, которые расположены от точки испытания хⁱ не дальше, чем от остальных точек испытаний х^k, k = 1,2, …, N, k ≠ i.

Точка хⁱ называется неулучшаемой в квадрате D относительно системы узлов Х_N, если не существует сколь угодно близкой к ней точки х’ такой, что

A_i(x’) = A_i(xⁱ). (6.14)

В противном случае (при нарушении неравенства (6.14)) точка хⁱ называется улучшаемой точкой, а процедура замены ее точкой х’ — улучшением.

Введенные определения позволяют описать алгоритм F³⁶, реализующий пассивный поиск на двумерном квадрате D точки глобального минимума х*, в виде следующей последовательности действий.

1. Задаются любая произвольная система узлов Х_N = (х¹,…, х^N) и вид нормальной функции ρ(х, хⁱ) (например, ρ(х, хⁱ) = ||х — хⁱ||).

2. Для каждой точки испытания хⁱ, i = 1, 2, …, N, вычисляется максимальное расстояние, допустимое в ее области Дирихле:

A_i = max ρ(х, хⁱ). (6.15)

3. Из системы узлов X_N выделяется та из улучшаемых точек, которая удовлетворяет условию

A_k(x^k) = max А_j(х^j),

где максимум берется только по улучшаемым точкам х^j, j = 1, …, M.

4. Если в системе узлов Х_N все точки хⁱ являются неулучшаемыми точками, тогда процесс построения оптимального покрытия (6.12) закончен и задача (6.1) считается решенной. В противном случае вычисления продолжаются с п. 5.

5. Последовательной процедурой улучшения производится замена точки х^k. полученной на п. 2, на неулучшаемую точку х’ и рассматривается новая система узлов, для которой все вычисления повторяются с п. 2.

Для любой точки xⁱ нормальная функция ρ(х, хⁱ) достигает своего максимального значения на границе области Дирихле S(xⁱ) в характерны точках, под которыми понимаются следующие точки (рис. 6.5):

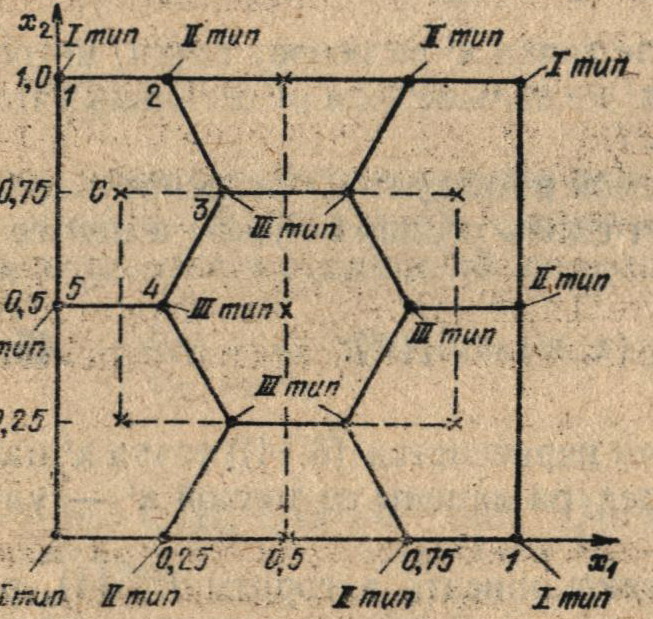
Рис. 6.5. Оптимальное покрытие квадрата семью кругами одинакового радиуса r* = 0,275 (сплошными линиями выделены области Дирихле для каждой точки испытаний, отмеченной крестиком)

1 тип — точки, являющиеся вершинами квадрата D;
2 тип — точки пересечения с границей области D линий.

Тогда процедура второго шага алгоритма может быть сведена к следующей последовательности действий:
1. Определяются все характерные точки {х^p} системы узлов.
2. Для каждой точки испытания xⁱ выделяются те характерные точки х^p, которые находятся к точке хⁱ ближе, чем к любой другой точке испытаний x^k, k = 1, 2, …, N, k ≠ i (так называемые действительные характерные точки):

ρ(х^p, хⁱ) ≤ ρ(х^p, х^k) для всех k = 1, 2,…, N

(например, на рис. 6.5 для точки испытания С действительными характерными точками являются точки 1 — 5).

3. Для каждой точки хⁱ в ее действительных характерных точках вычисляется функция ρ(х^p, хⁱ) и среди полученных значений выбирает-
ся максимальное в качестве параметра

A_i = A_i(хⁱ) = max ρ(х, хⁱ).

Перед началом работы алгоритма все точки системы узлов X_N считаются улучшаемыми, т. е. начальные значения признака α_i принимаются равными нулю для всех точек испытаний х¹,…, х^N. При замене улучшаемой точки х^k на неулучшаемую точку х’ (п. 5) параметр принимает значение, равное единице. Для любой другой точки х’ новой системы узлов (6.16) принимается α_i = 0, если значение ρ(х, хⁱ) в тех характерных точках области Дирихле S(хⁱ), где ρ(х, хⁱ) = А_i изменилось больше, чем на заданную величину δ, определяющую точность построения оптимального покрытия. Если α_i = 1 для всех точек испытаний х’, i = 1, 2,…, N, то процесс поиска точки минимума x* закончен (п. 4). В противном случае, из тех точек испытаний, для которых α_i = 0, для улучшения выбирается точка х^k, которой соответствует наибольшее значение параметра A_k = A_k (х^k) (п. 3).

Процедура улучшения точки испытания х^k на пятом шаге алгоритма представляет собой последовательный процесс, на каждом этапе которого необходимо определить достаточно малый вектор перемещения Δ^k = (Δx₁^k, Δx₂^k) такой, чтобы

A_k(x^k + Δ^k) < A_k(x^k). (6.20)

При этом надо потребовать, чтобы для значений A_i остальных точек испытаний, которые могут уменьшиться, сохраниться или возрасти, выполнялось условие

A_i(xⁱ) < A_k(x^k + Δ^k), i=1,2, …, N, i≠k.

Комментарии запрещены.