Алгоритмы получения сигналов с заданными статическими свойствами
В задачах имитационного моделирования систем, подверженных действию случайных сигналов, важное место принадлежит воспроизведению реально действующих сигналов. Задача заключается в еле дующем: располагая видом и параметрами корреляционной функции и закона распределения математически заданного или реально действующего сигнала (полученного на основе обработки реализаций по экспертным данным) разработать алгоритмы, позволяющие создавать модели случайных сигналов, имеющих близкие к ним соответствующие статические характеристики.
Псевдослучайный сигнал, полученный выше, может быть использован при имитационном моделировании как вид статистической помехи, шума. Но генератор псевдослучайных сигналов может быть использован и для получения на ее основе сигналов с заданными статистическими свойствами.
Схема получения сигналов с заданными статистическими свойствами
Общая схема получения таких сигналов дана на рисунке ниже:
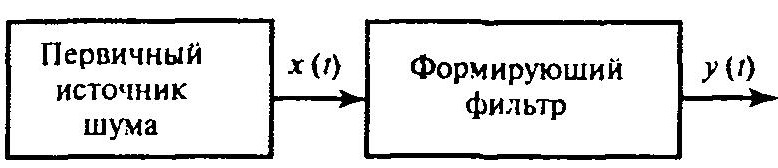
Рис. Схема получения сигналов с заданными статистическими свойствами
В качестве первичного источника шума x(t) используем генератор ПСДП, а формирующий фильтр-синтезатор можно представить в виде некоторого дискретного фильтра (рисунок ниже).

Рис. Генератор ПСДП
В основе реализации схемы лежит представление произвольного сигнала в виде
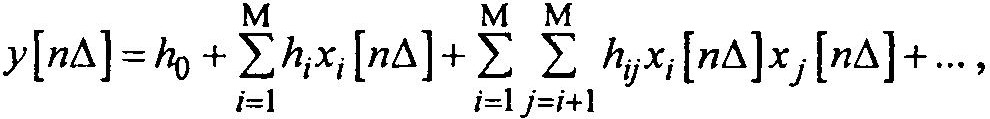
т.е. через соответствующие суммы с весами при выбранной базовой функции. В качестве базовой функции здесь используется хi [nΔ] — псевдослучайная последовательность, снимаемая с i-й ячейки регистра сдвига, с весовыми коэффициентами hi, hij при соответствующих членах разложения а m < M <2m -1 = N.
Формула по существу представляет собой некоторое отображение, которое реализуется схемой.
Цифровой фильтр осуществляет суммирование взвешенных сигналов, снимаемых с первичного генератора шума. Задача синтеза фильтра заключается в подборе необходимых значений весовых коэффициентов.
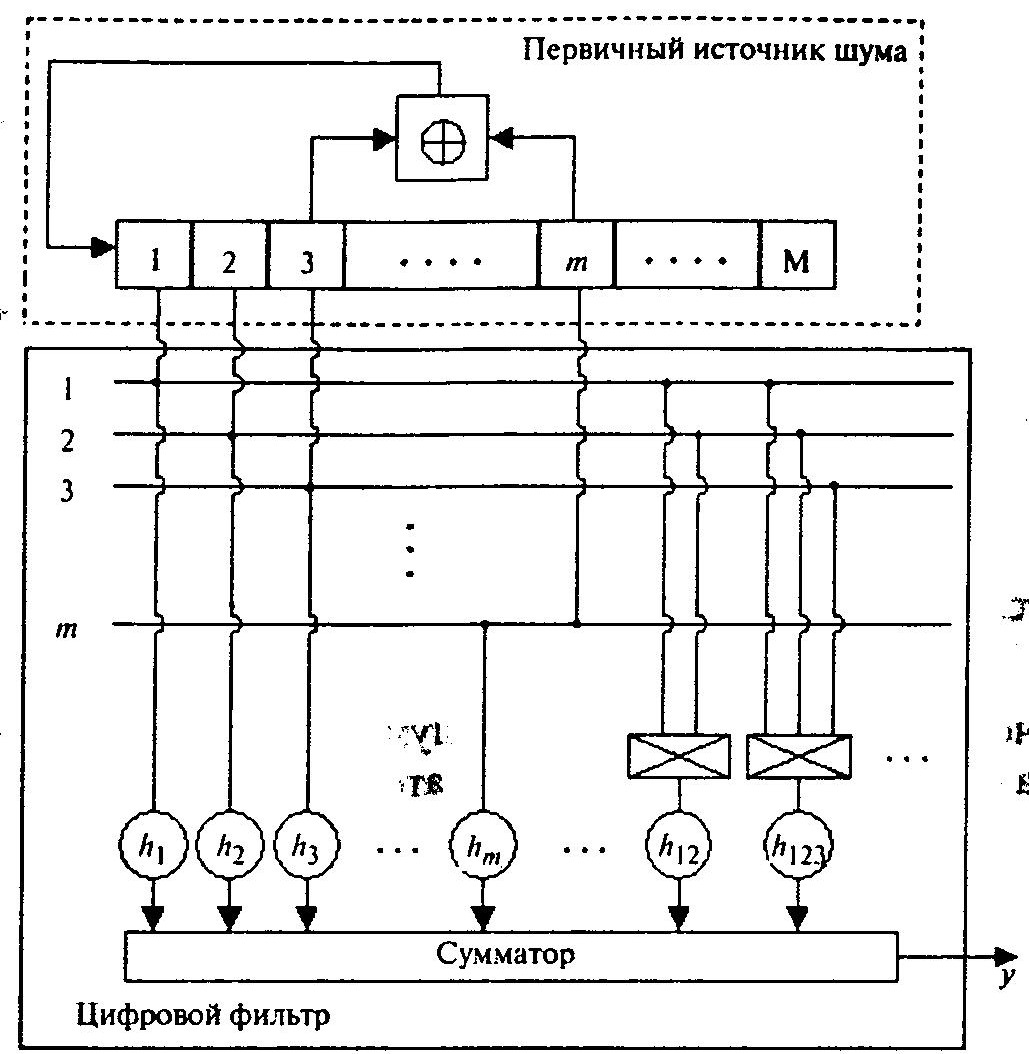
Рассмотрим конкретные алгоритмы выбора весовых коэффициентов для требуемых видов законов распределения и корреляционных функций.
Алгоритм получения сигнала с заданным законом распределения
Рассмотрим алгоритм при аппроксимации искомого сигнала первой суммой в разложении, а именно
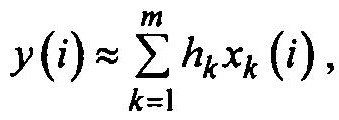
где i — номер такта; xk(i) — псевдослучайная двоичная последовательность, снимаемая с k-й ячейки генератора; hk — весовые коэффициенты.
Введем в рассмотрение характеристическую функцию ξ(v), однозначно связанную с законом распределения W(x):
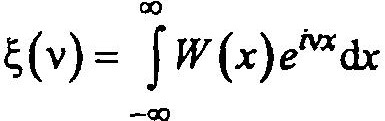
Тогда
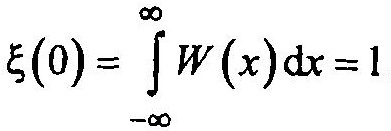
Из свойств псевдослучайной двоичной последовательности следует, что плотность распределения вероятностей (закон распределения) Wk (х) сигнала, снимаемого с к-й ячейки генератора и взвешенного с весом hk , имеет вид:
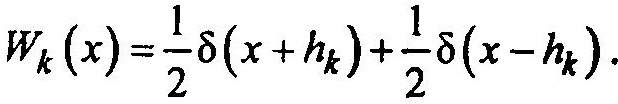
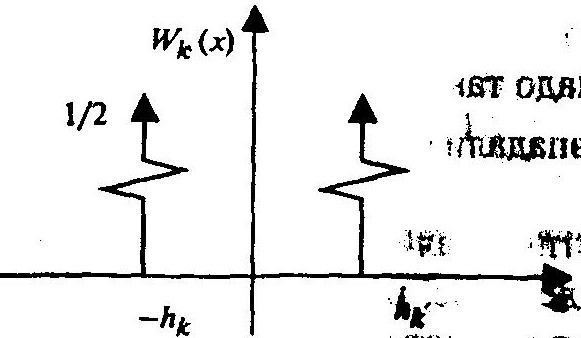
Тогда выражение для соответствующей характеристической функции примет вид (после соответствующих подстановок):
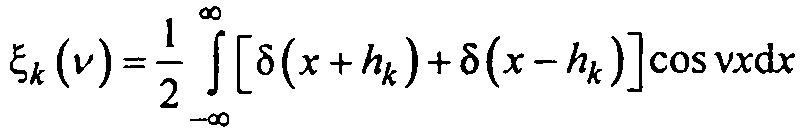
или
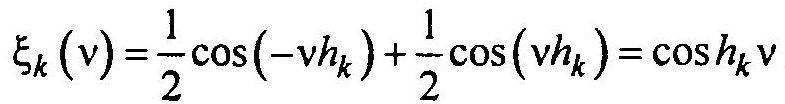
Так как сигналы, снимаемые с каждой из m ячеек практически статистически независимы, то сумме m независимых сигналов будет соответствовать характеристическая функция
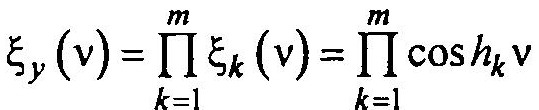
т.е. в области изображений сумма переходит в произведение.
Итак, задача получения сигнала с заданной плотностью распределения Wзад сводится к задаче нахождения весовых коэффициентов, обеспечивающих наилучшую аппроксимацию соответствующей характеристической функции выражением.
Другими словами, необходимо, чтобы площади под соответствующими характеристическими функциями были близки:
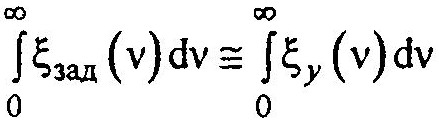
Можно сказать и так — вид характеристической функции конкретного сигнала определяет способ выбора коэффициентов hk.
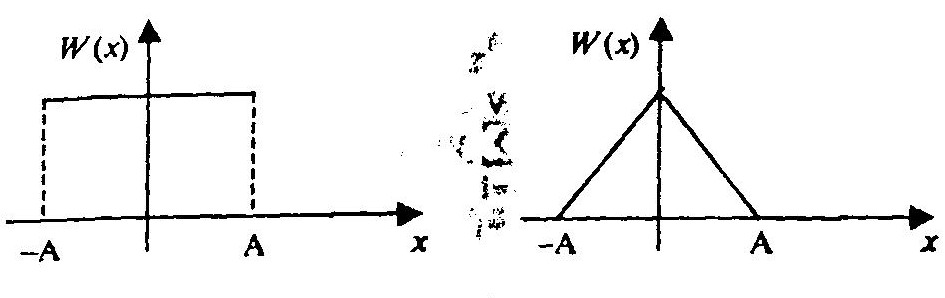
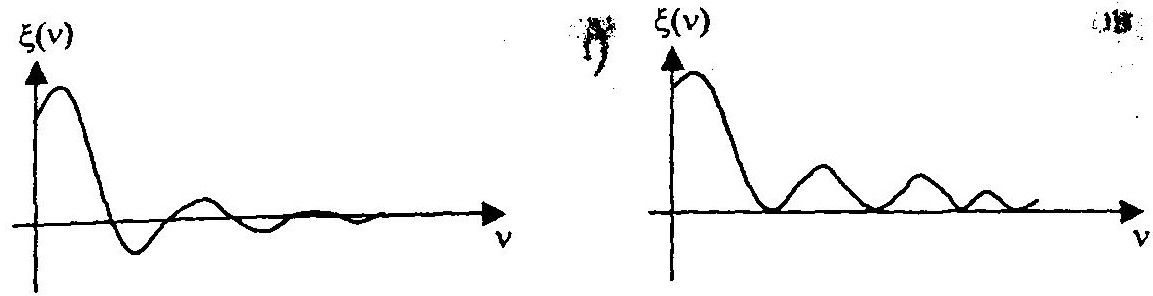
Рассмотрим равномерный и треугольный законы распределения и соответствующие им характеристические функции.
Здесь имеют место периодически повторяющиеся нули. Значение нулей определяют поведение ξ(v) во всей области изменения v.
Следовательно, надо так подбирать hk, чтобы нули у, определяемы формулой, совпадали с нулями требуемой характеристической функции.
Если характеристическая функция монотонная и не имеет нулей (нормальное распределение, распределение Лапласа, Коши), то хорошая аппроксимация получается, если положить
h1 = h2 = … = hk = h, т.е. все веса одинаковы.
В этом случае ξ(v) = cosm (hv) и задача выбора значения h решается посредством приближения площадей под кривыми
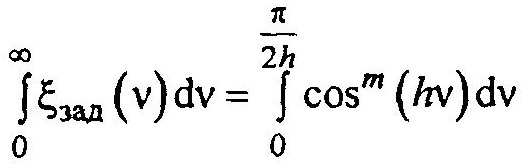
Для оценки точности можно использовать критерий вида:
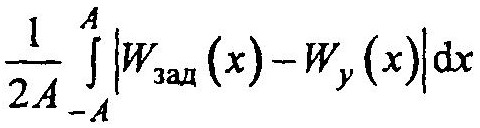
что характеризует величину средней абсолютной ошибки, с которой воспроизводится требуемая функция Wзад (х).
Решение задачи можно свести к табличным интегралам.
Алгоритм получения сигнала с заданной корреляционной функцией
Перепишем уравнение в эквивалентной форме
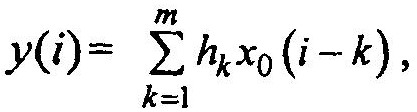
где х0 — последовательность на входе первой ячейки регистра; i-k — сдвиг на к тактов. Для стационарных случайных процессов справедливо эргодическое свойство (среднее по множеству равно среднему по времени).
Поэтому
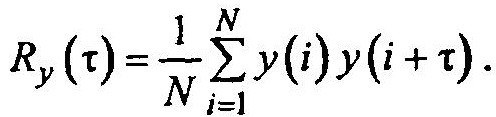
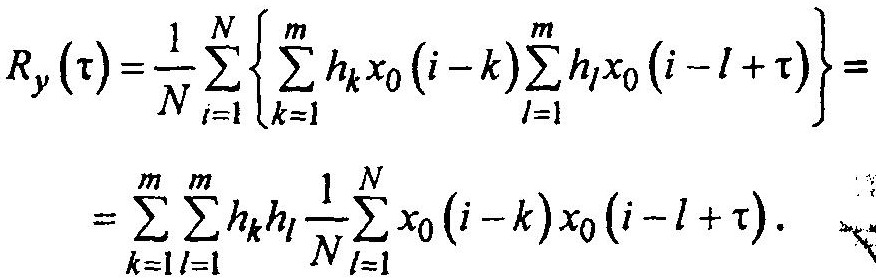
Сдвиг во второй сумме составит (i — l + τ) — (i — k) = k — l + τ. Эта сумма представляет собой корреляционную функцию Rх0 =(k- l +x) сигнала X0.
Поскольку х0 — это М-последовательность, то при k — l + τ=0
RX0 (0) = 1, а для остальных значений RX0 = 0, то перепишем в виде
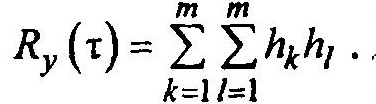
Окончательно имеем
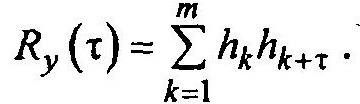
Таким образом, значения корреляционной функции искомого сигнала определяются численными значениями весовых коэффициентов, распределённых вдоль регистра сдвига. Как найти требуемые значения этих коэффициентов?
Для этого обратимся к Z-преобразованию корреляционной функции
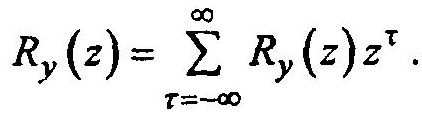
Подставив уравнение:
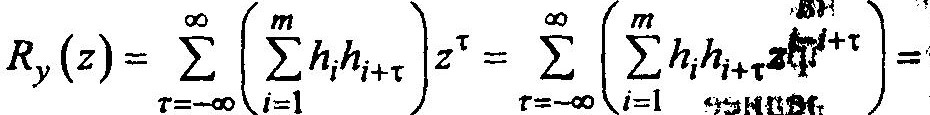
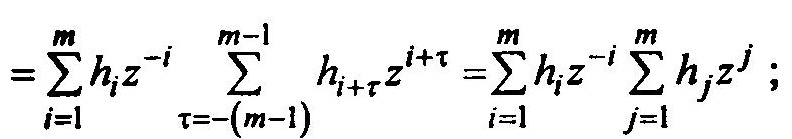
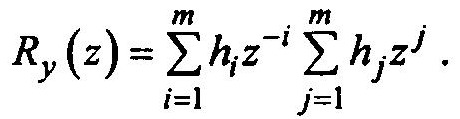
Можно представить Ry(z) как произведение полиномов от z.
Обозначим эти полиномы соответственно h(1/z) – первая сумма в формуле и h(z)— вторая сумма.
Для определения требуемых значений весовых коэффициентов используется специфическая многошаговая процедура деления
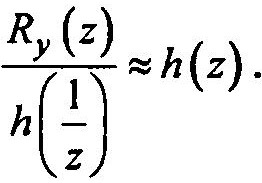
Это деление осуществляется до тех пор, пока соответствующие коэффициенты при h(1/z) и h(z) не будут близки с точностью до заданной погрешности (например, 0.05).
Полученные значения hk устанавливаются в схеме генерации. Тогда генератор выдает требуемый сигнал y[n].
Таким образом, для получения сигнала с заданной корреляционной функцией необходимо:
1) задать автокорреляционную функцию в виде совокупности ординат;
2) определить делением полиномов значение весовых коэффициентов и установить их в генераторе;
3) получить сигнал y[n];
4) определить погрешность результата.