Другой подход к решению задачи локализации точки глобального минимума X* многопараметрической функции Q (x₁, x₂, …, x_n) связан с использованием коллектива независимых стохастических автоматов как некоторой системы поисковой оптимизации.

Пусть имеется совокупность стохастических автоматов A_j, j = 1, 2, …, n, которые помещены в одну и ту же среду (в нашем случае это минимизируемая функция Q (x₁, x₂, …, x_n). Будем считать, что форма поведения j-го автомата является простейшей в том смысле, что все значения входа автомата y(r) разбиваются в зависимости от реакции среды связанной со знаком приращения минимизируемой функции ΔQ(x), на два типа:

y(r) = 1, если ΔQ = [Q(x^r+1 — Q(x^r)] ≤ 0 — благоприятная реакция среды (выигрыш);
y(r) = 0, если ΔQ = [Q(x^r+1) — Q(x^r)] > 0 — неблагоприятная реакция среды (штраф).

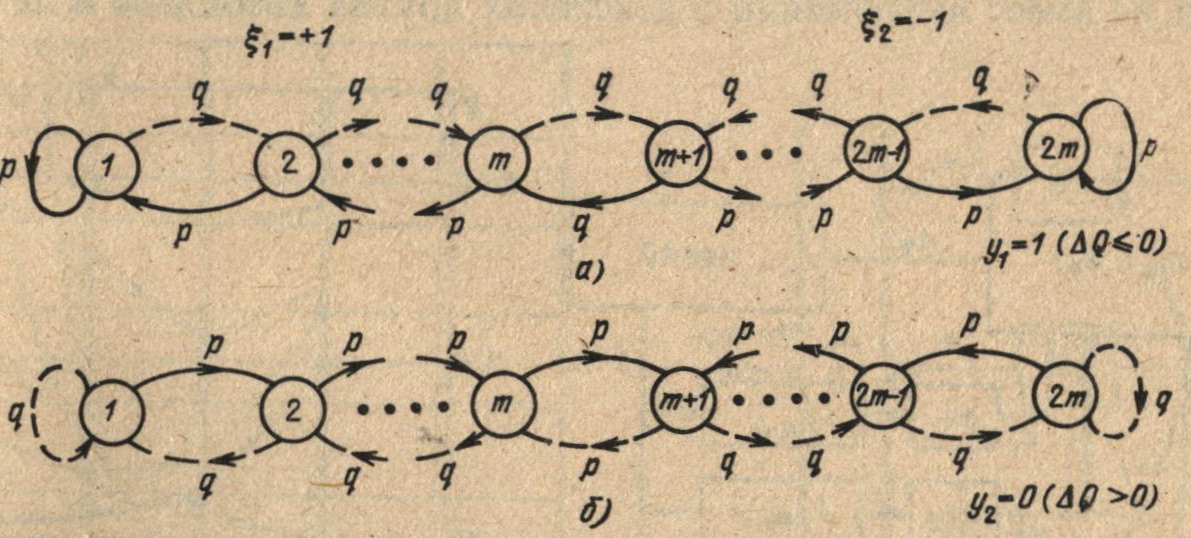
Рис. 6.10. Граф внутренних состояний стохастического автомата с линейной тактикой L_2m,2(p)

В свою очередь, действия автомата A_j, определяемый его внутренними состояниями S(r), пусть также имеют всего два значения. Например, для стохастического автомата с линейной тактикой L_2m,2(p). граф внутренних состояний S которого изображен на рис. 6.10, можем записать:

ξ_j(r+1) = +1 при 1 ≤ S(r+1) ≤ m;
ξ_j(r+1) = -1 при 1 < S(r+1) ≤ 2m; (6.39)

Здесь из 2m состояний автомата левые состояния 1 ≤ S(r+1) ≤ m соответствуют действию ξ¹(r + 1) = +1, а правые состояния m + 1 ≤ S(r+1) ≤ 2m — действию ξ²(r + 1) = -1. Параметр m называется глубиной памяти автомата. При благоприятной реакции среды (y(r + 1) = 1 для ΔQ < 0) с вероятностью p смена состояния происходит в соответствии со сплошными стрелками, а с вероятностью q = 1 - р(q < p) - соответствии с пунктирными (рис. 6.10, а). При неблагоприятной реакции среды (у(r + 1) = 0 для ΔQ > 0) смена состояний происходит наоборот (рис. 6.10, б). Если р = 1 (в этом случае q = 0), то стохастический автомат L_2m,2(р) превращается в детерминированный автомат с линейной тактикой L_2m,m. Так, при m = 1 автомат L_2,2 сохраняет свое состояние при выигрыше (у(r + 1) = 1) и меняет его при штрафе (у(r + 1) = 0).

Образуем систему, состоящую из коллектива автоматов L_2m,2ⁱ(р), i = 1, 2, …, n. Они работают независимо друг от друга и взаимодействуют со средой (функцией Q(х)) путем изменения на (r + 1)-й итерации i-й переменной по формуле

x_i(r+1) = x_i(r) + Δx_i(r+1) = x_i(r) + λ_iξ_i(r+1). (6.40)

Здесь λ_i — длина шага вдоль i-гo координатного направления I_i, ξ_i(r + 1) — действие i-го автомата на (r + 1)-м шаге, равное +1 или — 1 в зависимости от реакции среды у (r + 1) и от того, находится ли автомат в одном из первых m состояний (S (r) = 1, 2, …, m) или в одном из последних состояний (S(r) = m + 1, …, 2m). Согласно (6.40) каждый автомат автономно в силу своей внутренней структуры организует направленное движение к точке минимума х* (положительно реагируя на уменьшение функции Q (х) и отрицательно на ее возрастание), а затем случайно блуждает в его окрестности. Каждый автомат не имеет информации о действиях других автоматов и не способен непосредственно изменить эти действия. Взаимодействие автоматов осуществляется только через среду (функцию Q (х)), реагирующую на их совместные действия значением приращения ΔQ.

Алгоритм реализующий глобальный поиск с помощью коллектива независимых автоматов с линейной тактикой L_2m,2, может быть представлен в виде системы поисковой оптимизации (будем называть ее автоматным оптимизатором), приведенной на рис. 6.11.

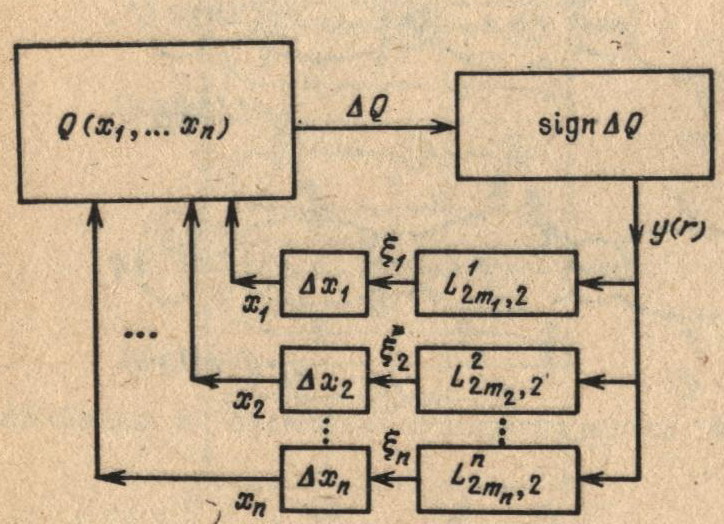
Рис. 6.11. Структурная схема системы поиска минимума с помощью коллектива независимых автоматов L_2m,2(p)

Входной переменной для каждого автомата является одна и та же реакция среды у(r + 1), определяемая согласно формуле (6.39) по знаку приращения минимизируемой функции Q (х). Все автоматы A_i, i = 1,2, …, n, считаются однотипными и засинхронизированными по поступлению входного воздействия и по смене внутренних состояний.

Коллектив одинаковых (m_i = m₀, λ_i = λ, i = 1,2, …, n), симметричных, детерминированных автоматов с линейной тактикой L_{2m, m} поиска минимума не осуществляет. Это связано с выходом всех автоматов на синхронный режим, в котором последние изменяют свои выходные действия на противоположные одновременно после m₀ итераций, что приводит к колебательным движениям, при которых значение функции Q (х) периодически повторяется. Поиск коллективом независимых детерминированных автоматов возможен только при условии их разнообразия, например различной глубине памяти.

Разнообразие автоматов может быть обеспечено путем введения в их поведение элементов случайности. Поэтому в дальнейшем будем считать, что автоматный оптимизатор (рис. 6.11) состоит из коллектива независимых стохастических автоматов L_2m,2ⁱ(р), i = 1, 2, …, n, каждый из которых определяется тремя одинаковыми параметрами: m_i = m — глубиной памяти; p_i = р — вероятностью смены внутренних состояний и λ_i = λ — длиной шага, связанного с изменением i-й переменной. В качестве критериев, оценивающих эффективность процесса поиска глобального минимума функции Q (х) с помощью алгоритма F⁴⁰, будем рассматривать следующие характеристики:

Q* = Q*(m, р, λ) — среднее значение функции Q(х) в окрестности точки глобального минимума х*;
δ = δ (m, p, λ) — среднеквадратичное отклонение функции Q (х)
от ее среднего значения Q*(m, р, λ);
N = N (m, p, λ) — среднее число испытаний, необходимое для перехода автоматного оптимизатора из начальной точки х° в окрестность точки глобального минимума х*.

Введенные характеристики в сильной степени зависят от параметров автоматов. На рис. 6.12 приведены зависимости среднего.числа испытаний N от глубины памяти m (при p = 0,9 и λ = 0,1), из которых видно, что для различного числа переменных n оптимальная глубина памяти имеет разные значения.

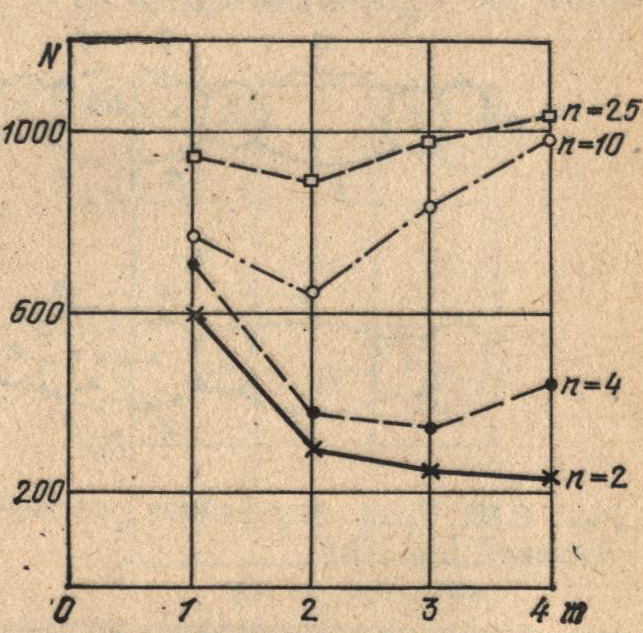
Рис. 6.12. Зависимость среднего числа испытаний от глубины памяти автомата m.

Это связано с тем, что слишком маленькая глубина памяти приводит к «рысканию», а слишком большая глубина памяти — к «инерционности» автоматов. Зависимость погрешности поиска (дисперсионности) δ имеет экспоненциальный характер от величины вероятности р (рис. 6.13, где n = 2, λ = 0,1).

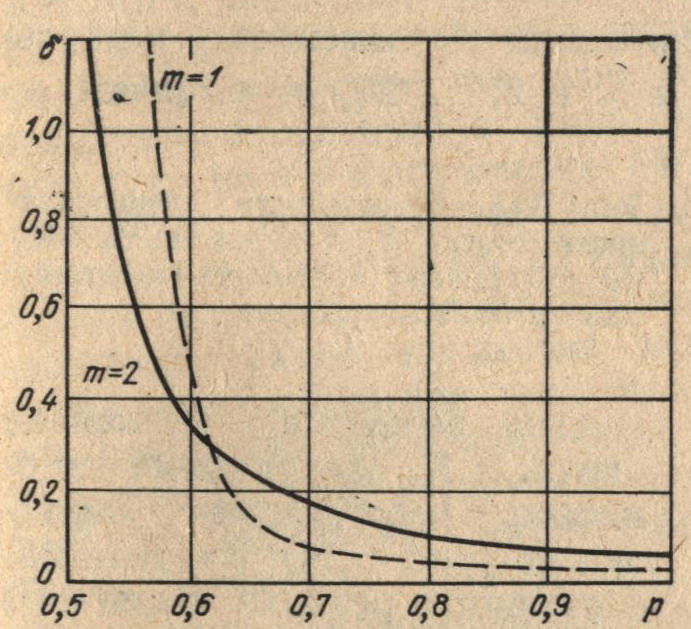
Рис. 6.13. Зависимость дисперсионности поиска δ от вероятности смены внутренних состояний автомата р

Из рис. 6.13 видно, что при р → 0,5 величина δ → ∞, т. е. чем «безразличнее» автоматы к точке минимума (при р = q = 0,5 движения автомата как к точке минимума, так и от нее являются равновероятными), тем на большую величину может изменяться соответствующая переменная, что и обеспечивает автоматному оптимизатору свойство обнаружения точки глобального минимума.

Эффективность алгоритма может быть повышена за счет дублирования работы автоматов по каждой из координат (каналу автоматного оптимизатора) и «рассинхронизации» смены ими внутренних состояний.

При дублировании каждый из автоматов A_i заменяется несколькими «автоматами-дублерами» A_i^k, k = 1, 2, …, N_i, т. е. поиск по каждой переменной ведется не одним, а N_i одинаковыми автоматами, работающими параллельно (рис. 6.14).

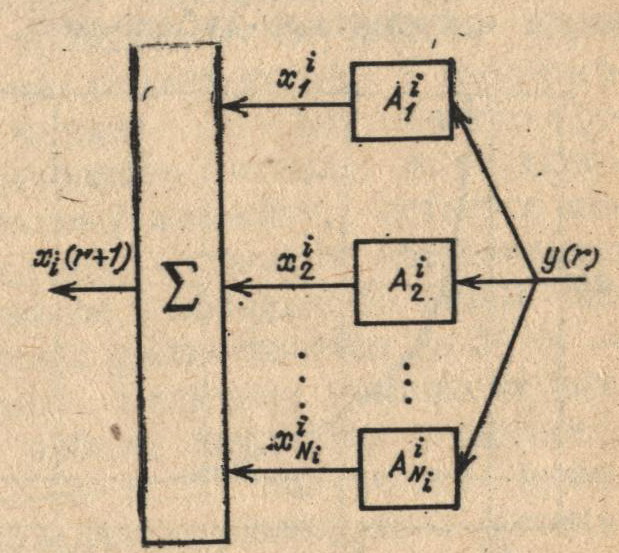
Рис. 6.14. Дублирование N_i автоматов, работающих на i-м канале автоматного оптимизатора

Входная информация о реакции среды у(r) является общей для всех автоматов, а выходное действие ξ_i(r + 1) совокупности из N_i; автоматов-дублеров является средним арифметическим значением действий каждого из автоматов ξ_i^k(r + 1):

ξ_i(r+1) = 1/N_i ∑ξ_i^k(r+1)

Это приводит к тому, что при неодинаковом числе автоматов-дублеров приращение Δx_i (r + 1) = λ_iξ_i(r + 1) по каждой координатной оси I_i будет иметь разные значения, зависящие от числа дублеров N_i. В связи с этим увеличивается разнообразие поисковых движений автоматного оптимизатора.

Кроме обеспечения поисковых возможностей коллектива автоматов, дублирование повышает надежность работы всей системы. Экспериментальные исследования показывают, что поиск минимума осуществляется, если выходят из строя несколько «дублеров», но при этом остается достаточное число исправно работающих дублирующих автоматов. На рис. 6.15 показана зависимость погрешности поиска δ от вероятности р неисправных автоматов-дублеров при минимизации функции двух переменных и использовании по каждой переменной четырех автоматов-дублеров (по три исправных с р = 0,9 и одному неисправному автомату).

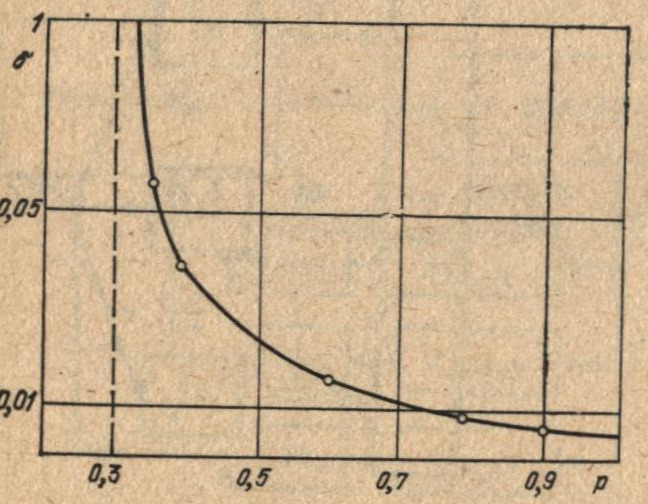
Рис. 6.15. Зависимость дисперсионности поиска δ от вероятности смены внутренних состояний неисправных автоматов-дублеров

При изменении р от 1 до 0,4 поиск минимума имеет место. Лишь при значениях р*, близких к 0,3 (при отсутствии дублирования р* ~ 0,5), система теряет поисковые возможности в связи с неограниченным ростом погрешности поиска δ. Устойчивая работа системы при поломке нескольких автоматов-дублеров объясняется тем, что в окрестности точки минимума на выходе исправных автоматов поддерживаются значения, которые в сумме с выходными сигналами неисправных значений дают правильные значения координат точки минимума, т. е. исправные автоматы подстраиваются к работе неисправных таким образом, чтобы компенсировать неправильную работу последних.

Работа автоматов в системе поиска минимума, изображенной на рис. 6.11, синхронизирована во времени, т. е. все автоматы меняют свои внутренние состояния и выдают выходные сигналы одновременно. Теперь допустим, что моменты выдачи выходных сигналов автоматами, входящими в коллектив, происходят случайным образом, т. е. на k-м шаге поиска i-й автомат выдает сигнал с вероятностью p_i и с вероятностью (1 — p_i) не меняет своего внутреннего состояния и, следовательно, не выдает выходного сигнала, т. е. координата x_i(r + 1), соответствующая данному автомату, остается постоянной. Такой коллектив независимых автоматов обеспечивает асинхронное изменение выходных сигналов и обладает большим числом поисковых движений, число которых увеличивается до 3³ (n — размерность минимизируемой функции). Величина компонент вектора р’ определяет интенсивность работы автоматов в процессе поиска минимума. При p_i = 1, i = 1, 2, …, n, получается прежняя система синхронизированного коллектива независимых автоматов.

Комментарии запрещены.