Задачи и методы оптимизации в системах моделирования играют вспомогательную, но важную роль — они призваны решать, в основном, задачи параметрической оптимизации.

В задачах оптимизации требуется получить наилучший набор значений параметров или функций с учетом накладываемых на них ограничений. Ограничения могут быть прямыми и функциональными. Наличие ограничений приводит к условной оптимизации, к условному экстремуму. Решение задач при наличии ограничений называют математическим программированием (линейное, квадратичное и нелинейное). Для получения решения необходимо сформулировать целевую функцию, которая выражает зависимость оптимизируемого критерия от параметров оптимизации.

Здесь уместно отметить, что модульное построение проблемно-ориентированного языка (ПОЯ) моделирования систем имитации позволяет легко конструировать необходимые целевые функции. Целевая функция должна позволять находить оптимум аналитическим или численным способом.

Из многих форм целевой функции самой распространенной является квадратичная форма, определяемая в виде суммы квадратов разностей между желаемым решением и решением при текущих значениях оптимизируемых величин. На практике могут встретиться задачи одномерной (один варьируемый параметр) и многомерной оптимизации.

Известны методы одномерной оптимизации — методы золотого сечения, Фибоначчи и многомерной оптимизации — градиентные методы, методы наискорейшего спуска и др. Бывают поисковые и беспоисковые процедуры оптимизации. Методов оптимизации много. Большое число методов оптимизации — признак слабости, а не силы. При решении практических задач надо уметь выбрать наиболее подходящий метод, что сделать не просто.

В инженерной практике нашел себя поисковый метод Розенброка. Этот метод хорошо приспособлен, когда целевая функция представляет собой узкий овраг (или гребень), произвольно расположенный по отношению к варьируемым переменным (см. рисунок ниже).

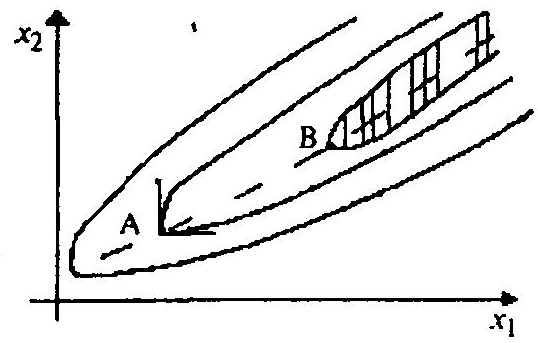
Здесь метод покоординатного движения Гаусса—Зейделя не работает, плохо работает метод случайного поиска и др.

Появление оврагов или гребней является результатом того, что целевая функция объединяет в себе конфликтные входные переменные, тенденции которых могут быть противоположными.

Метод Розенброка является развитием метода покоординатного движения. Последний метод эффективен, когда линия оврага (гребня) оказывается параллельной одной из координатных осей. Именно это свойство метода покоординатного движения и используется в методе Розенброка. Он основан на повороте координатных осей в процессе поиска для создания удобного взаимного расположения оврага (гребня) и системы координат.

Для поворота осей координат используется информация, получаемая во время поиска (рисунок ниже).

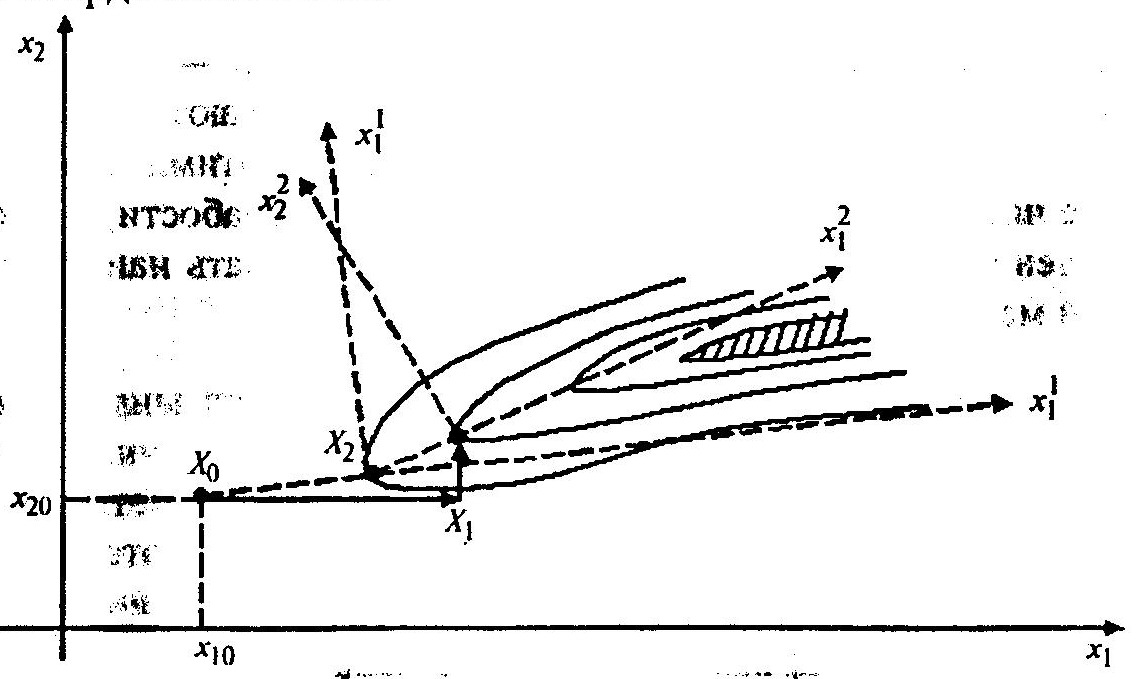
После первого цикла поиска вдоль осей х₁ и х₂ из начальной точки Х₀ получаем точку Х₂ направление вектора Х₂ — Х₀ принимается за новое направление первой координатной оси. В общем случае другие координатные оси пристраиваются исходя из условий взаимной ортогональности. Следующий цикл поиска идет уже вдоль нового направления координатных осей.

В литературе метод Розенброка иногда называют методом вращающихся координат. Поиск каждого промежуточного экстремума по выбранному направлению осуществляется следующим образом: шаг увеличивается в 3 раза, если продвижение вдоль выбранного направления было успешным, и меняется на обратное с уменьшением шага в 1,5 раза в противном случае.

Правило прекращения процесса поиска состоит в выполнении одного из условий:
1) число оценок целевой функции достигло максимально заданного значения;
2) продвижение за цикл поиска меньше заданной величины.
Относительным недостатком метода Розенброка является сравнительно большое время поиска.

Различные современные процедуры оптимизации представлены в ряде программных комплексов методов оптимизации. Хорошо известна диалоговая система оптимизации ДИСО, разработанная в ВЦ Академии Наук, и упомянутая ранее система MathCad.

Комментарии запрещены.