Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом (ПФЭ). Число возможных сочетаний уровней (или число опытов) определяется по формуле N = pⁿ, где р — число уровней; п — число факторов.

Рассмотрим свойства и особенности факторного планирования на простых примерах.

Пример 1
Полный фактор эксперимента при n = 2 и p = 2. Рассмотрим описание модели второго порядка
Y = b₀x₀ + b₁x₁ + b₂х₂ + b₃х₃ + b₄x₄ + b₅х₅.

Число строк (опытов) в матрице планирования N = 2² = 4, а максимальное число столбцов — 6. Собственно план эксперимента определяется числом факторов — их два X₁ и Х₂. Остальные столбцы матрицы планирования являются производными столбцов х₁ и x₂. План эксперимента формируется так, чтобы выполнить условие ортогональности — сумма элементов каждого столбца плана эксперимента должна равняться нулю, т.е.

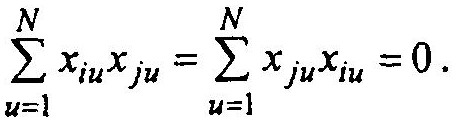
Это достигается чередованием знаков в столбце х₁, а в каждом последующем столбце плана эксперимента частота чередования вдвое уменьшается по сравнению с предыдущим столбцом.

Отметим особенность матрицы планирования. Исходная модель требует определения шести коэффициентов (b₀ — b₅), Следовательно, должно быть шесть уравнений (или шесть столбцов). Но различных столбцов всего четыре, что соответствует числу строк.

Однако число различных столбцов равно числу членов аппроксимирующего полинома (*), включая все возможные взаимодействия (в нашем примере одно взаимодействие b₁₂x₁x₂). Вывод ПФЭ 22 позволяет определить все коэффициенты полинома при линейных членах и всех возможных взаимодействиях факторов (включая в общем случае взаимодействие максимально высокого порядка x₁, x₂, …, x_n).

То, что столбцы 4 и 5 одинаковы и совпадают с нулевым столбцом свидетельствует о том, что рассматриваемый ПФЭ (и все ПФЭ 2ⁿ) не позволяет определить все коэффициенты, в частности коэффициенты при X_i², точнее невозможно независимо определить коэффициенты b₀, b₁₁ и b₂₂, т.е. получается смешанная оценка коэффициентов.

Такие планы ПФЭ называют планами первого порядка, так как они позволяют определить коэффициенты лишь при факторах в первой степени.

Отсюда вытекает практическая рекомендация — в планах ПФЭ 23 и больших степеней нет смысла формировать столбцы для квадратов факторов x_i.

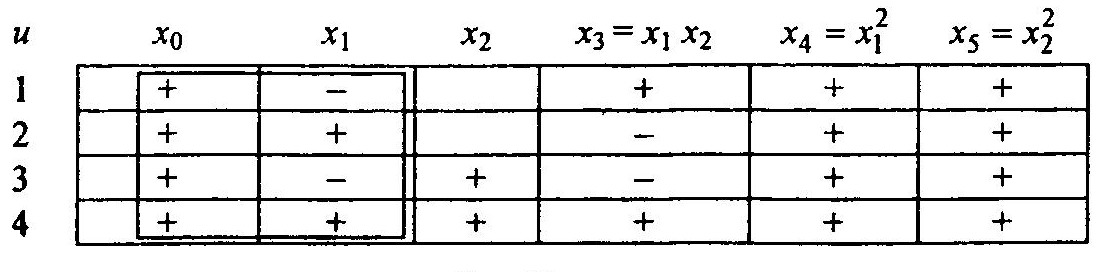
Пример 2. Полный фактор эксперимента при n = 3 и p = 2. Модель принимает вид
Y = b₀ + b₁x₁+b₂x₂+b₃x₃+b₄x₄+b₅x₅+b₆x₆+b₇x₇

В этом случае N=2³=8, т.е. будет восемь строк в матрице планирования.

Из матриц планирования следует характерное для ПФЭ 2ⁿ соотношение

т.е. сумма квадратов значений факторов в каждом столбце равна числу опытов N. С учетом этого формула (5.11) для вычисления коэффициентов упрощается и принимает вид

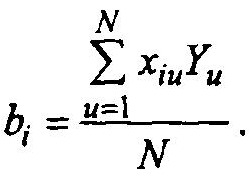
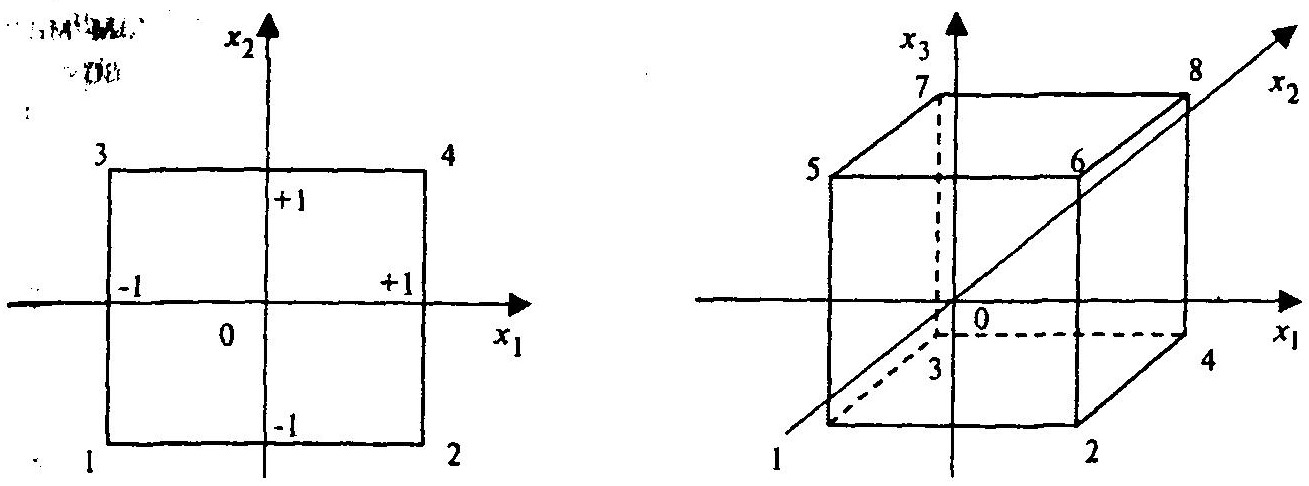
Точки планов ПФЭ 2ⁿ располагаются в вершинах квадрата, куба или в общем случае гиперкуба.

Анализируя ПФЭ рⁿ, легко заметить, что с ростом числа уровней факторов р и, особенно, с ростом числа факторов n число опытов, предусмотренных планом, будет существенно превышать число искомых коэффициентов, т.е. ПФЭ дает избыточную информацию. Можно ли более экономно организовать эксперимент? Это можно сделать посредством рассмотрения дробных реплик ПФЭ.

Комментарии запрещены.