Множества и операции над ними
Понятие множества неопределимо. Пусть A, B, C –произвольные множества. a, b, c-их элементы. Основными не определяемыми отношениями в математике являются: a=b, a принадлежит множеству A. Введём следующее отношение:
A⊆B⇔∀a(a∈A→a∈B)
A=B⇔A⊆B&B⊆A
A⊂B⇔A⊆B&A≠B
A⊇B⇔B⊆A
A⊃B⇔A⊇B& A≠B
Введём обозначения: P(A)– множество всех подмножеств множества A. Перечеркнутый кружок — пустое множество и само множество А называются несобственными (тривиальными) подмножествами множества А.
Определим операции (функции) над множествами: A или B={x: x принадлежит A и x принадлежит B}
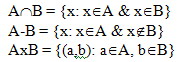
Декартово произведение A и B.
Замечание: Операции пересечения, объединения, разности множеств называются булевыми. Булевы операции и декартово произведение можно распространить на несколько сомножителей:
A1xA2x…xAk={(a1,a2,…,ak):a1 принадлежит A1, a2 принадлежит A2,…, ak принадлежит Ak}
Пусть A, B, C есть произвольные подмножества некоторого универсального множества U (универсум).
Пусть не(A)=U-A (дополнение A до U). Иногда обозначают по другому.
Тогда справедливы следующие (булевы) свойства операций над множествами:
1. Идемпотентность (A и A) =A, (A или A)=A.
2. Коммутативность (A и B) = (B и A), (A или B) = (B или A).
3. Ассоциативность A и (B и C) = (A и B) и C, A или (B или C)=(A или B) или C.
4. Правило поглощения A и (A или B)=A, A или (A и B) = A.
5. Дистрибутивность A и (B или C)=(A и B) или (A и C), A или (B и C)=(A и B) или (A и C).
6. Инволюция не (не(A))=A.
7. Свойство констант (A и U) = A, (A или U) = U, (A и пустое множество) = пустое множество, (А или пустое множество) = A.
8. Закон исключённого третьего и закон противоречия (A или не(A)) = U, (A и не(A)) = пустое множество.
9. Не (А и В) = (не (А) или не (В)), не (А и В) = (не (А) или не (В)).
Перечисленные свойства доказываются непосредственно, как равенство двух множеств.