Графы и группы подстановок, орбита группы подстановок
Определение: Группа есть множество G с определенными на нем операциями: X*Y : GxG→G и взятие обратного элемента x-1: G→G и выделенным элементом 1 или е, удовлетворяющее следующим аксиомам: ∀x, y, z ∈ G:
1. x*(y*z) = (x*y)*z
2. ∃e∈G e*x = x*e = x
3. ∀x∈G ∃x-1∈G x*x-1 = x-1*x = e
Определение: Группа называется коммутативной (Абелевой), если х*у = у*х (* — умножение). Группа с умножением называется мультипликативной, а группа со сложением – аддитивной.
Определение: Если множество А={1,2,…,n} постоянно, то взаимнооднозначное отображение р:А →А называется подстановкой, которая обозначается:
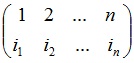
где ik = p(k). Произведение двух подстановок есть их последовательное исполнение.
Множество подобных подстановок, определенных на множестве А с операциями умножения подстановок и взятия обратной подстановки образуют симметрическую группу Sn с единицей:

которая есть тождественная подстановка. Заметим, что симметричная группа Sn не коммутативна и содержит n! элементов.
Пусть Sn есть симметрическая группа подстановок, определенных на множестве Х={1,2,…,n}.
Утверждение: Всякая конечная группа порядка n(число элементов в группе) изоморфна некоторой подгруппе симметрической группы Sn.
Пусть G=(p0=e,p1,…,pr} есть некая группа подстановок, определенная на множестве X={1,2,…,n} с единицей p0=e (тождественной подстановкой).
Введём отношение X~Y на Х так, чтобы X~Y ⇔ ∃p∈G (p(x)=y)
X~Y есть отношение эквивалентности, то есть он удовлетворяет трем аксиомам:
1. X~X
2. X~Y ⇒ Y~X
3. X~Y и Y~Z ⇒ X~Z
Замечание: Отношение X~Y индуцирует разбиение множества Х на попарно непересекающиеся классы эквивалентных между собой элементов.
Определение: Класс эквивалентности в множестве Х по отношению к соотношениям X~Y называется орбитой группы подстановок G. Длина орбиты есть число её элементов.
Замечание: Для ∀а ∈Х множество А(а)={р0(a)=a, р1(a),…,рn-1(a)} перечисляет все элементы, эквивалентные а, и потому множество А(а) есть орбита группы G.
Замечание: Орбита О замкнута относительно ∀ функции р(х)∈G, то есть ∀a∈O ∀P∈G р(a)∈O.
Утверждение: ∀O={i1,…,iu} группа подстановок G для ∀ элемента с∈О орбита О=А(с)={р0(с)=с, р1(с),…,рn-1(с)}
Следствие: Все орбиты группы подстановок G исчерпываются орбитами вида А(а).
Замечание: Множество Х={1,2,…,n} распадается в сумму попарно непересекающихся между собой орбит группы G.