Многочлен циклов (цикловой индекс), теорема Пойа
Пусть G есть группа подстановок множества Х={1,2,…n} и пусть конечное множество Y={1,2,…,m} имеет не менее двух элементов. Пусть есть множество всех функций из Х в У. (Х→У).
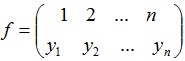
Число таких функций обозначается |Y||X| всех наборов из m=|Y| множества Y с n=|X| элементов в каждом наборе. Пусть подстановка р из G действует на функцию f из М и дает функцию g=p(f)=pf в соответствии с равенством. (pf)(x)=g(x)=f(p(x)). Каждая подстановка р из G определяет подстановку на множестве функций Y*. pM(fi) = pMfi = p(fi). Обозначим множество таких подстановок через GM.
Например, X = {1, 2, 3, 4}, Y = {1, 2, 3}.
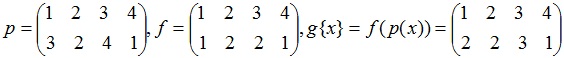
— как последовательное исполнение двух подстановок.
Действие подстановки pM на функцию f сводится к перестановке значений функции f в соответствии с подстановкой p. Произведение подстановок из GM определяется как результат их последовательного применения. Тождественная подстановка есть 1 в множестве GM. Обратная подстановка (pM-1g)(x) = g(p-1(x)) = f(p(p-1(x))) = f(x). Следовательно, GM есть группа. Она называется степенной группой, порожденной группой G.
G есть группа подстановок на множестве Х={1,2,…,n}. Каждую подстановку можно представить в виде множества непересекающихся циклов. Пусть степень skr означает, что подстановка имеет r циклов длины k. Обозначим через jk(p) число циклов длины k в подстановке р. Полином циклов или цикловой индекс Z(G) группы G есть полином от n переменных s1, s2, … , sn, определяемый формулой Z(G) = Z(G, s1, …, sn) = |G|-1∏∑skjk(p).
Наибольшую длину цикла имеет подстановка (1,2,…,n), состоящая из единственного цикла длины n=|X|. Поэтому полином циклов имеет n переменных s1, s2, … , sn. Подстановка:
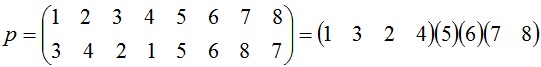
соответствует произведению s12s2s4. G={(1)(2)(3),(1)(23),(2)(13),(3)(12),(123),(132)}. На множестве Х={1,2,3} имеем многочлен циклов Z(G)=Z(G,s1,s2,s3)= 1/3! (s13 + 3s1s2 + 2s3).
Теорема: (Пойа). Пусть G есть группа подстановок порядка r на множестве объектов Х={1,2,…,n} и множестве Y={1,2,…,m}. Число орбит степенной группы Gm, действующей на множестве функций из Х→У, получается заменой каждой переменной в полиноме циклов Z(G) на m.
N(G) = Z(G, s1, …, sn) = |G|-1∑∏skjk(p)