Определение: Поле (F,+,*) есть множество F элементов произвольной природы с определенными на нем двумя операциями сложением λ + μ: FxF → F и умножением λ * μ: FxF → F, удовлетворяющих следующим аксиомам:
∀λ, ν, μ ∈ F (F – есть абелева группа со сложением):
1) λ+(μ +ν)= (λ+μ) +ν
2) ∃x ∈ F λ+x = μ
3) ∃y ∈ F y +λ =μ
4) λ+ μ = μ + λ

F без нуля есть абелева группа по умножению:
5) λ*(μ*ν) = (λ*μ)*ν
6) ∃x ∈ F (λ*x = μ, λ ≠ 0)
7) ∃y ∈ F (y*λ = μ, λ ≠ 0)
8) λ*μ = μ*λ
9) λ*(μ + ν) = λ*μ+ λ*ν (дистрибутивность)

Пример:
E2={0,1}.

Объект F = (E2,+,*) – есть поле

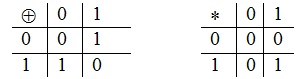
Замечание: элемент –1 равный 0-1 = такому λ, что 0=1+λ откуда λ=1 ⇒
-1 =1 (mod 2)

Определение: Линейное пространство L над полем F есть множество L элементов произвольной природы с двумя операциями: сложение a+b: L x L → L и умножением на const из F λ*a: FxL → L (λ*a = a*λ), удовлетворяющие следующим аксиомам: ∀a, b, c ∈ L, ∀λ, μ ∈ F
1) a+(b+c) = (a+b)+c,
2) a+b = b+a,
3) ∃0 ∈ L: a+0=a,
4) ∀a ∈ L ∃(-a) ∈ L: a+(-a) = 0,
5) λ(a+b) = λa+λb,
6) (λ+μ)a = λa+μa,
7) λ(μa) = (λμ)a,
8) 1*a =a, 1 ∈ F.

Пример:
Пусть E₂ⁿ – есть множество всех векторов a=(a₁, a₂,…,a_n), длины n из нулей и единиц. Введем линейное правило L₂ⁿ векторов из E₂ⁿ над двухэлементным полем F=(E2,+,*) со сложением и умножением по mod₂ определив поразрядное сложение и умножение векторов на константу {0,1} положив:
∀a, b ∈ E₂ⁿ, ∀λ∈ E₂ a+b = (a₁+b₁, a₂+b₂,…, a_n+b_n), λ*a = (λ*a₁, λ*a₂,…, λ*a_n).

E₂⁴: a=(1,0,0,1), b = (0,1,1,1)
a+b = (1,1,1,0),
a*0 = (0,0,0,0),
1*a = (1,0,0,1).

Комментарии запрещены.