Определение: Граф G = (V,E) называется двудольным графом (биграфом), если множество V его вершин допускает разбиение на 2 непересекающихся подмножества V1 и V2 (две доли). Причем каждое ребро графа соединяет вершины из различных долей. Обозначается через G = (V1,V2,E) – двудольный граф с долями V1 и V2. Будем считать, что |V1| ≤ |V2|.

Определение: Двудольный граф G = (V1,V2,E) есть полный двудольный граф, если каждая вершина из V1 соединена ребром с каждой вершиной из V2. Обозначается через K_m,n – полный двудольный граф G = (V1,V2,E), у которого n= |V1|, m = |V2|. Звезда – полный двудольный граф K_1,p.

Теорема: граф G – двудолен ⇔ все простые циклы в G имеют четную длину(четное число ребер).

Необходимость⇒: пусть граф G = (V,E) = (V1,V2,E) двудолен. И пусть C = v₁e₁v₂e₂v₃e₃v₄…v_n-1e_n-1v_n (v₁ = v_n) есть простой цикл в G длины n-1. Тогда v₁, v₃, v₅, v₇ ∈ V1, а v₂, v₄, v₆, v₈₁ ∈ V2, т.е. вершины с нечетными номерами лежат в V1, а с четными в V2. Т.к. v_n=v₁, то v_n – нечетен. Тогда длина цикла n-1 есть четное число.

⇐Достаточность: Пусть G = (V,E) есть граф, в котором все простые циклы имеют четную длину. Можно считать, что граф G связен, ибо каждая компонента связности графа G может рассматриваться по отдельности. Пусть v₁ ∈ V есть произвольная вершина в связном графе G и пусть множество вершин V₁ = {v∈V: расстояние между v и v₁ — четно}, тогда V₂ = V– V₁ есть множество вершин находящихся от v₁ на нечетном расстоянии. Покажем, что всякие две вершины в V₂ не могут быть соединены в G ребром. Допустим противное: пусть пара вершин u,v ∈ V₂ соединена в G ребром e=(u,v). Пусть [v₁, u] и [v₁, v] – есть две геодезические (нечетной длины) линии. Тогда [v₁, u] ∪ {e} ∪ {v, v₁} – есть простой цикл в G нечетной длины. А это есть противоречие с условием.

Следовательно любые две вершины в V2 несмежны. Аналогично можно показать, что любые две вершины в V1 также несмежны. Поэтому ребра в графе G соединяют вершины из разных множеств V1,V2, => граф G двудолен. Доказано.

Паросочетания

Определение: Паросочетание есть двудольный граф, в котором всякие два ребра не являются смежными.

Паросочетание P для графа G=(V,E) есть всякое множество попарно несмежных ребер в G. P есть наибольшее паросочетание для G, если число ребер в Р наибольшее среди всех паросочетаний для G и P есть максимальное (тупиковое) паросочетание для G, если всякое добавление ребра к Р делает Р не паросочетанием.

P – есть совершенное паросочетание для G, если P имеет мощность |V| вершин (покрывает все вершины из V).

Замечание: Наибольшее паросочетание – максимально. Совершенное паросочетание является наибольшим и максимальным.

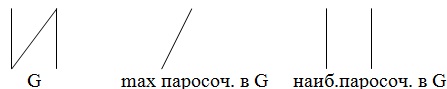
Простая цепь С ненулевой длины в G, ребра которой попеременно лежат и не лежат в P, называется чередующейся цепью (относительно паросочетания P). Эта цепь С называется P-увеличителем, если первое и последнее ребра цепи лежат вне Р. С помощью Р-увеличителя С паросочетание Р может быть переделано в другое паросочетание P’ для G с числом ребер в Р’ на единицу больше, чем в Р. Для этого достаточно все ребра в С, лежащие вне Р, добавить в Р, а ребра в С, лежащие в Р, удалить из Р. Для получившегося паросочетания Р’ можно снова искать увеличитель и т.д., последовательно расширяя полученное паросочетание, пока это возможно.

Теорема: если паросочетание Р для графа G не является наибольшим, то граф G имеет Р – увеличитель.

Доказательство: Если паросочетание Р, которое задается множеством его ребер для G, то G имеет другое паросочетание Р’ с большим числом ребер, чем в Р. В подграфе графа G, образованном множеством вершин (Р-Р’)U(P’-P) степень каждой вершины не больше 2. Следовательно, каждая компонента связности этого подграфа есть простая цепь ( простой цикл) с чередующимися ребрами из Р и из Р’.

Среди этих компонент можно найти простую цепь нечетной длины, начинающуюся и заканчивающуюся ребрами из Р’, иначе |P’|<|P|. Противоречие. Поэтому эта цепь - Р-увеличитель в G. Следствие: если граф G не имеет Р-увеличителя, то паросочетание Р для графа G является наибольшим.

Теорема: Граф G=(V,E) имеет совершенное паросочетание <=> для ∀v’⊆V , где n(G-v’)≤|V| есть число таких компонент связности подграфа G-v’ графа G, которые имеют нечетное число вершин.

Алгоритм построения совершенного паросочетания для двудольного графа
Пусть G = (U,V,E) – двудольный граф. Выберем исходное паросочетание P₁ (наПример одно ребро графа G). Допустим, что паросочетание P_i = (U_i,V_i,E_i) для G построено.

Построим паросочетание P_i+1 для G следующим образом.
1) Выберем u из U но не из Pi. Если такой вершины u нет, то P_i – совершенное паросочетание. Строим в G чередующуюся цепь μ_i = (u₁v₁u₂v₂,….. u_pv_p) c u₁ = u в которой всякое ребро (u_i,v_i) не принадлежит E_i. А всякое ребро (v_i,u_i+1)∈ E_i, Если такой цепи нет, то совершенного паросочетания граф G не имеет, а паросочетание P_i является для графа G максимальным. Цепь μ_i есть Р_i-увелечитель.
2) Выбрасываем из P_i все ребра (v_i, u_i+1) и добавляем все ребра (u_i,v_i) цепи u_i. Получившееся паросочетание Pi+1 на одно ребро длиннее паросочетания P_i.
3) GOTO 1.

Комментарии запрещены.