Аналитические методы расчета надежности ТЭС и АЭС
В основу аналитических методов расчета надежности энергетических установок положены два подхода.
Первый основан на использовании логических схем:
• метод дерева отказов;
• метод минимальных путей и сечений.
Второй – на использовании моделей пространства состояний:
• метод перебора состояний;
• марковская модель.
Условием применимости первой группы методов является существование логической схемы и независимости отказов элементов. Все методы позволяют получить только стационарные вероятности работы или отказа системы за длительный период. Кроме того, логические схемы можно построить только для относительно простых систем.
Вторая группа методов расчета надежности основана на вычислении вероятностей и частот состояний, выборе критериев и условий отказа системы. Эти методы требуют более сложного математического аппарата и позволяют получить нестационарные значения показателей надежности. При их использовании законы распределения вероятностей отказов и восстановлений элементов, как правило, принимаются экспоненциальными. Представление элементов в двух состояниях (работа-отказ) в этом случае не обязательно.
Метод перебора состояний
Методы расчета последовательных, параллельных и смешанных соединений – основа расчета надежности любого объекта. Однако не всегда, в том числе в энергетике, удается свести структуру объекта к этим классическим видам соединений, и тогда прибегают к более сложным методам расчета.
Рассмотрим, например, мостиковую схему:
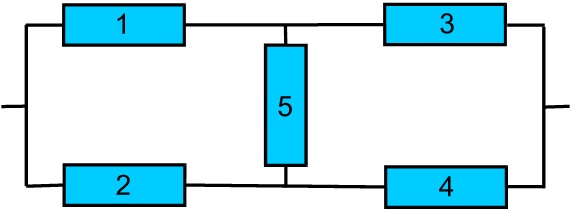
Подобным образом могут быть соединены трубопроводы подвода пара к турбине, причем элементы 1, 2, 3 и 4 тогда представляют собой участки паропроводов с арматурой, а элемент 5 – уравнительную перемычку.
Метод перебора состояний реализует следующие этапы расчета надежности:
• выявление множества возможных состояний;
• расчет вероятностей этих состояний.
Определяют два непересекающихся множества состояний, отвечающих работоспособному и неработоспособному состояниям всей системы. Каждое из этих состояний характеризуется набором элементов также в рабочем и отказавшем состояниях. При независимых отказах вероятность каждого состояния определяется произведением вероятностей нахождения элементов в тех или иных состояниях.
Тогда вероятность работоспособного состояния системы равна
P = ∑[∏pl∏qk]
где m – общее число работоспособных состояний, в каждом j из которых число исправных элементов равно lj, число вышедших из строя — kj, а аргумент t опущен в этом примере (но он есть на самом деле!)
Сведем в таблицу все возможные работоспособные состояния схемы, отмечая знаком «+» работоспособное состояние каждого из пяти элементов схемы и знаком «-» неработоспособное состояние. В каждом из j состояний системы комбинация работоспособных элементов, помеченных знаком «+» в таблице, обеспечивает пропуск пара через мостиковую схему трубопроводов, несмотря на отказ остальных элементов. Предположим для простоты вычислений, что вероятности безотказной работы всех элементов одинаковы и равны p1=p2=p3=p4=p5=p=0.9, а вероятности отказа соответственно q1=q2=q3=q4=q5=q=0.1.
Выполнив прямой перебор возможных работоспособных состояний, просуммируем значения вероятностей pj этих состояний и получим искомую вероятность безотказной работы данной системы:
Номер j состояния системы Состояние элементов Вероятность pj состояния системы
| Номер j состояния системы | Состояние элементов | Вероятность pj состояния системы | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 1 | + | + | + | + | + | p1⋅p2⋅p3⋅p4⋅p5=0.95 |
| 2 | — | + | + | + | + | p2⋅p3⋅p4⋅p5⋅q1=0.94⋅0.11 |
| 3 | + | — | + | + | + | p1⋅p3⋅p4⋅p5⋅q2= 0.94⋅0.11 |
| … | … | … | … | … | … | … |
| 16 | + | — | + | — | — | p1⋅p3⋅q2⋅q4⋅q5= 0.92⋅0.13 |
P = p5 + 5p4⋅q + 8p3⋅q2 + 2p2⋅q3=0.978
Метод разложения относительно особого элемента
Этот метод гораздо компактнее предыдущего. Он предусматривает выделение в объекте одного элемента, все возможные состояния которого образуют полную группу состояний системы. В мостиковой схеме (см. рис.) удобно выбрать в качестве «особого» элемент 5 – перемычку.
Если элемент 5 безусловно исправен, получаем систему:
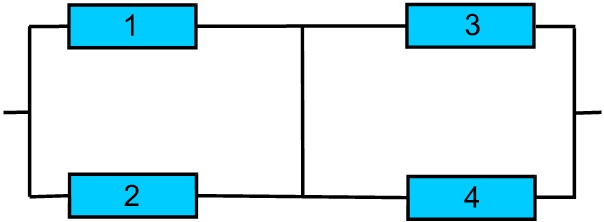
для которой вероятность безотказной работы составляет
[1-(1-p1)(1-p2)]⋅[1-(1-p3)(1-p4)] при вероятности безотказной работы элемента 5, равной p5. Поэтому вероятность безотказной работы такого соединения равна P1= p5[1-(1-p1)(1-p2)]⋅[1-(1-p3)(1-p4)].
Если элемент 5 безусловно неисправен, то получаем следующую систему:
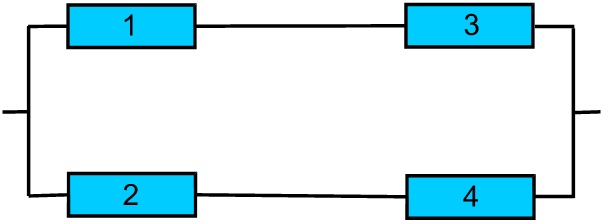
для которой вероятность безотказной работы равна [1-(1-p1p3)(1-p2p4)], а вероятность нахождения элемента 5 в неисправном состоянии равна (1- p5), так что вероятность безотказной работы соединения в данном случае составляет P2=(1- p5) [1-(1-p1p3)(1-p2p4)].
Вероятность безотказной работы рассматриваемой мостиковой схемы является суммой вероятностей двух рассмотренных состояний при выделенном особом элементе: P= P1+ P2.
Пусть вероятность безотказной работы всех элементов равна p=0.9, тогда P1=0.882, P2=0.096 и следовательно P=0.978.
Таким образом, результат расчета совпадает с предыдущим, но получен существенно более простым способом.
Метод минимальных путей и сечений
Этот метод применяется только для систем с монотонной структурой, свойства которых формулируются следующим образом:
• система работоспособна, если все элементы работоспособны;
• система находится в состоянии отказа, если все элементы отказали;
• при отказе элемента состояние системы только ухудшается.
Минимальный путь – это такое множество элементов, при нормальной работе которых система работоспособна, а отказ любого из этих элементов приводит к отказу системы.
Минимальное сечение – это такое множество элементов, отказ которых приводит к отказу системы, но работоспособное состояние любого из них обеспечивает работоспособное состояние системы при условии работоспособности элементов, не входящих в данное минимальное сечение.
В общем случае система может иметь несколько минимальных путей и минимальных сечений. Любую структурную схему можно представить в виде параллельного соединения минимальных путей или в виде последовательного соединения минимальных сечений. Только система из последовательно соединенных элементов имеет единственный минимальный путь.
Этот метод дает не точные значения показателей надежности, а граничные (интервальные) оценки этих показателей сверху и снизу. Во многих случаях, особенно для сложных систем, подобных оценок оказывается достаточно.
Рассмотрим метод минимальных путей и сечений на примере. Необходимо рассчитать вероятность безотказной работы системы трубопроводов с перемычкой, структурная схема которой представлена мостиковой схемой. Надежность элементов системы одинакова и равна pi=0,9.
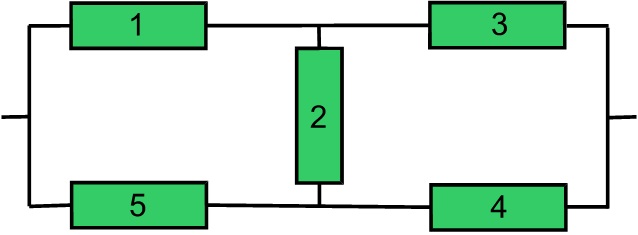
Сначала определяем минимальные пути для анализируемой схемы. Множество элементов, работоспособность которых обеспечивает работоспособность системы, следующие: {13}, {54}, {124}, {523}, {134}, {543}, {153}, {154}, {524}, {123}, {1524}, {1523}, {1234}, {5234}, {1354}, {15234}. Из них минимальными являются пути: 13, 54, 124, 523. Количество минимальных путей – 4.
Применительно к рассматриваемой схеме набор минимальных путей выглядит следующим образом:
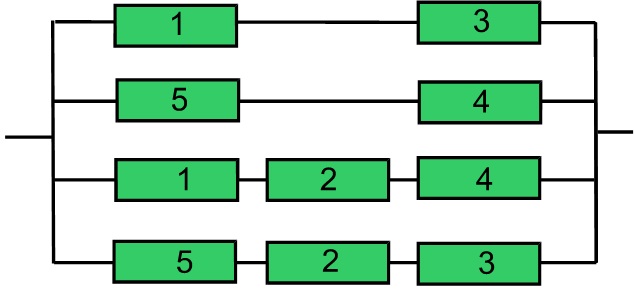
Вероятность безотказной работы такого соединения элементов дает оценку «сверху» вероятности безотказной работы исходной системы:
PB = 1 — (1 — p1p3)⋅(1 — p5p4)⋅(1 – p1p2p4)⋅(1 – p5p2p3)≈0,997.
Затем выделим минимальные сечения, т.е. такие варианты цепочек элементов, которые при отказе всех элементов цепочки дают отказ всей системы, несмотря на работоспособность остальных цепочек. Значит, цепочки соединены между собой последовательно, а поскольку при работоспособности любого из элементов внутри цепочки она обеспечивает работоспособность всей системы (при исправности остальных цепочек), то, следовательно, элементы в пределах цепочек соединены параллельно. Набор минимальных сечений выглядит следующим образом:

Вероятность безотказной работы набора минимальных сечений дает оценку «снизу» вероятности безотказной работы схемы.
PН = (1 — q1q5)⋅(1 – q3q4)⋅(1 – q1q2q4)⋅(1 – q5q2q3)
При вероятности отказа любого элемента схемы q=1 — p=0,1 получаем оценку снизу PН ≈ 0,978.
Обратим внимание, что PН ≈ 0,978 совпадает с результатом вычисления вероятности безотказной работы системы по приведенным ранее точным методам (метод перебора состояний и метод разложения относительно особого элемента).
Таким образом, согласно методу минимальных путей и сечений, оценка вероятности безотказной работы рассматриваемого соединения при заданных значениях показателей надежности его элементов находится в пределах
0,978 ≤ PC ≤ 0,997.
Метод «дерева отказов»
«Деревом отказов» называется логическая графологическая иерархическая схема, представляющая собой связь событий отказа системы с отказами элементов. Вершины дерева представляют собой логические операции типа И и ИЛИ (обозначающие соответственно произведение или сумму событий).
«Дерево отказов» начинается с конечного события, в качестве которого понимается полный отказ системы. На более низком уровне обозначаются события, которые вызывают конечное событие в соответствии с логической операцией, связывающей эти события. На нижнем уровне располагаются события отказов элементов.
Анализ «дерева отказов» заключается в определении такой комбинации элементов, одновременный отказ которых приводит к вершине дерева – отказу энергоустановки. В частных случаях может быть множество элементов, отказ которых приводит к отказу системы.
При анализе «дерева отказов» используются следующие стандартизированные логические символы:
«прямоугольник» — событие, которое является результатом нижерасположенных событий;
«дуга» — логическая операция ИЛИ, определяющая возникновение любого события на данном уровне, расположенном ниже вышестоящего уровня, и заканчивающаяся отказом на вышестоящем уровне;
«полуокружность» — логическая операция И, определяющая одновременное возникновение всех находящихся под этим знаком событий на данном уровне, расположенном ниже вышестоящего уровня, и заканчивающаяся отказом на вышестоящем уровне;
«окружность» — первоначальное событие, независимое от других.
Например на рисунке для функциональной схемы энергоблока (а) представлено соответствующее ей «дерево отказов» (б).
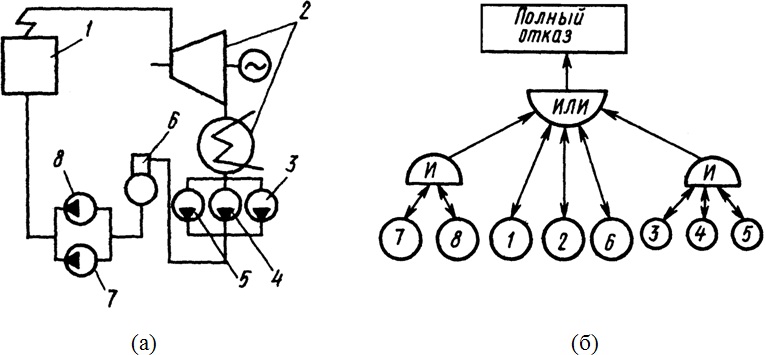
1- котел; 2- паровая турбина с конденсатором; 3, 4, 5 – конденсатные насосы; 6 – деаэратор; 7, 8 – питательные насосы.
Для рассмотренного примера множество элементов, отказ которых приводит к отказу системы, составит {1}, {2}, {6}, {7,8}, {3,4,5}. Это множество элементов называется сечением. Минимальное сечение – такое множество, из которого нельзя удалить ни одного элемента, иначе оно перестанет быть сечением. Если анализ «дерева отказов» начинать от конечного события, то при прохождении через вершину И увеличивается число элементов в сечении, а при прохождении через вершину ИЛИ – число сечений. Это дерево отказов содержит пять минимальных сечений 1, 2, 6, (7,8), (3,4,5). Если определено множество минимальных сечений, то вероятность отказа системы определится как сумма вероятностей отказов соответствующих сечений.
Метод «дерева отказов» включает следующие основные действия:
• определение системы и границ системы, которая должна быть проанализирована;
• определение самого нежелательного события в системе или состояния отказа системы;
• установление до «компонентного уровня отказов», которые приводят к указанному нежелательному событию или состоянию отказа системы.
Чтобы выполнить анализ безотказности, ремонтопригодности и готовности системы, для которой строится «дерево отказов», необходимо построить ее компонентную схему, что, в свою очередь, требует инженерного понимания анализируемой системы.
Принадлежность объекта к компоненте идентифицируется посредством двух условий:
• наличием показателей наработки на отказ и времени восстановления работоспособного состояния;
• возможностью только двух состояний: отказа или работоспособного состояния.