Основные теоремы теории вероятностей
На практике обычно требуется определить вероятность событий, непосредственное экспериментальное воспроизведение которых затруднено.
Обычно такая оценка и производится с целью выявления наиболее рациональных конструктивных параметров элементов перспективной техники.
Поэтому, как правило, для определения вероятностей событий применяются не непосредственные прямые методы, а косвенные, позволяющие по известным вероятностям одних событий определять вероятности других событий, с ними связанных.
Применяя эти косвенные методы, мы всегда в той или иной форме пользуемся основными теоремами теории вероятностей. Этих теорем две:
• теорема сложения вероятностей;
• теорема умножения вероятностей.
Введем понятие о сумме событий и произведении событий.
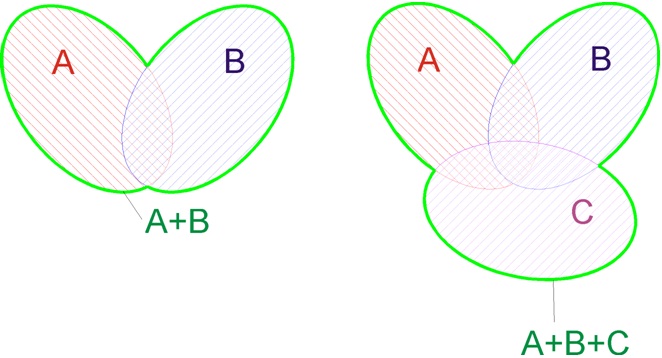
Суммой двух событий А и В называется событие С состоящее в появлении хотя бы одного из событий А и В. Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.
Геометрическая интерпретация:
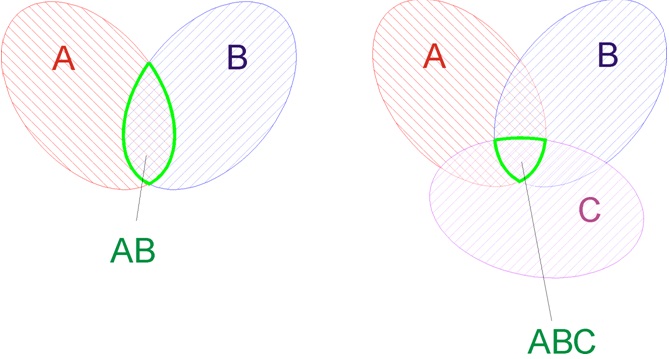
Произведением двух событий А и В называется событие С, состоящее в совместном выполнении события А и В. Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий.
Геометрическая интерпретация:
Теорема сложения вероятностей
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:
Р(А+В) = Р(А) + Р(В) (1)
Теорема сложения вероятностей применима к любому числу несовместных событий. В общем виде ее удобно записать:
Р(∑Ai) = ∑Р(Ai) (2)
Отметим следствия вытекающие из теоремы сложения вероятностей.
Следствие 1: Если события А1, А2, …, Аn образуют полную группу несовместных событий, то сумма их вероятностей равна единице:
∑Р(Ai) = 1 (3)
Перед тем как вывести второе следствие теоремы сложения, введем понятие «противоположные события».
Противоположными событиями называются два несовместных события, образующих полную группу. Событие противоположное событию А принято обозначать A.
Пример:
Событие А – безотказная работа всех элементов технической системы; A — отказ хотя бы одного элемента.
Следствие 2: Сумма вероятностей противоположных событий равна единице:
P(A) + P(A) =1 (4)
Следствие 2 есть частный случай следствия 1.
Вероятность суммы двух совместных событий выражается формулой:
Р(А+В) = Р(А) + Р(В) – P(AB) (5)
Аналогично вероятность суммы трех совместных событий вычисляется по формуле:
Р(А+В+С) = Р(А) + Р(В) + Р(С) – P(AB) – P(AС) – P(ВС) + Р(АВС) (6)
Общая формула для вероятности суммы любого числа совместных событий:
Р(∑Ai) = ∑Р(Ai) — ∑Р(AiAj) + ∑Р(AiAjAk) — (-1)n-1P(A1A2…An) (7)
где суммы распространяются на различные значения индексов i; i, j; i, j, k и т.д.
Из формул (5) и (6) можно записать аналогичную формулу для произведения событий
P(AB) = Р(А) + Р(В) – Р(А+В) (8)
Р(АВС) = Р(А) + Р(В) + Р(С) – P(A+B) – P(A+С) – P(В+С) + Р(А+В+С) (9)
Теорема умножения вероятностей
Введем понятие независимые и зависимые события.
Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.
Событие А называют зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается Р (А/В)
Пример:
В урне два белых и один черный. Два лица вынимают из урны по одному шару. Рассматриваются события: А- появление белого шара у 1-го лица; В – появление белого шара у 2-го лица.
Решение: Р(А) до того как произошло событие В равно 2/3. Если событие В произошло, то Р(А)=1/2. Таким образом, событие А зависит от события В.
Условие независимости события А от события В можно записать в виде:
Р(А/В) = P(A) (10)
а, условие зависимости: Р(А/В) ≠ P(A) (11)
Теорема умножения: Вероятность произведения двух событий равна произведению вероятности
Р(АВ) = P(A)⋅Р(В/А) (12)
Вероятность произведения нескольких событий равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется при условии, что все предыдущие имели место:
Р(А1А2…Аn ) = P(A1)⋅Р(А2/А1)⋅Р(А3/А1А2)⋅…⋅Р(Аn/А1А2…А n-1) (13)
Следствие 1: Если событие А не зависит от события В, то и событие В не зависит от события А
Следствие 2: Вероятность произведения двух независимых событий равна произведению вероятностей этих событий
P(AВ) = P(А)⋅Р(В) (14)
Р(А1А2…Аn ) = P(A1)⋅Р(А2)⋅….⋅Р(Аn) (15)
Формула полной вероятности
Следствием основных теорем является так называемая формула полной вероятности.
Пусть требуется определить вероятность некоторого события А, которое может произойти вместе с одним из событий:
Н1, Н2, ….Нn,
Образующих полную группу несовместных событий. Будем эти события называть гипотезами.
В этом случае, вероятность события А вычисляется как сумма произведений вероятности каждой гипотезы на вероятность события при этой гипотезе
Р(А)=∑Р(Hi)⋅P(A/Hi) (16)
Теорема гипотез (формула Бейеса)
Имеется полная группа несовместных гипотез Н1, Н2, …., Нn. Вероятности этих гипотез до опыта известны и равны соответственно Р(Н1), Р(Н2)…. Р(Нn).
Произведен опыт, в результате которого наблюдалось появление некоторого события А. Как следует изменить вероятность гипотез в связи с появлением этого события? По существу речь идет о том, чтобы найти условную вероятность Р(Нi/А) для каждой гипотезы.
Р(Нi/А) = [Р(Нi)⋅Р(Нi/A] / [∑Р(Hi)⋅P(A/Hi)], i = 1, 2, …, n (17)