Диффузия тепловых нейтронов
Связана с движением тепловых нейтронов в объеме. При возникновении разности значений плотностей тепловых нейтронов в разных точках объема появляется диффузионный ток (закон Фига). Вектор j — показывает в каком направлении и какой величины происходит переток нейтронов из одной точки в другую, вызванный разностью n1 > n2.
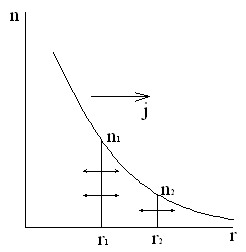
j = — D grad (n), D’ = ltrv/3;
j = — D grad (Ф), D = ltr/3;
• r232 = 2 laltrN1 — расстояние от точки появления до точки поглощения теплового нейтрона
• la — длина свободного пробега
• Ld = r23/√6 — длина диффузии
• Слабопоглощающая среда Ld>Ls — иначе сильнопоглощающая
Уравнение диффузии запишем из баланса нейтронов в произвольном единичном объеме активной зоны. Будем считать, что количество нейтронов в этом объеме будет меняться от интенсивности протекания трех процессов:
• Перетечка нейтронов из соседних объемов (диффузия)
• Поглощение нейтронов средой, находящейся в выделенном объеме
• Появление новых тепловых нейтронов вследствие замедления быстрых нейтронов
1/v ∂Ф/∂t = диффузия — поглощение + рождение
ΔФ = ∂2Ф/∂x2 + ∂2Ф/∂y2 + ∂2Ф/∂z2
1/v ∂Ф/∂t = DΔФ — ∑aФ + qT — дифференциальное уравнение диффузии тепловых нейтронов.
Т.к. замедление дискретно было введено понятие торможения. Надо записать, как меняется энергия нейтрона при торможении:
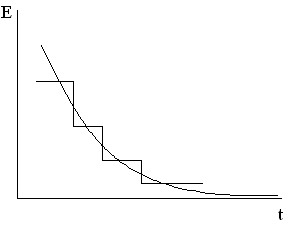
dE/dt = dE/dv ⋅ dv/dt, v — число соударений, dv/dt = v/ls = v ⋅ ∑S
ξ = d ln(E)/dv = 1/E ⋅ dE/dv ⇒ dE/dv = ξ⋅E
Получим dE/dt = ξEv∑s.
При записи уравнения диффузии примем допущения:
• В процессе замедления поглощение замедляющихся нейтронов отсутствует.
• Все быстрые нейтроны, рождающиеся в процессе деления, имеют одну и ту же энергию E0.
• Источники появления быстрых нейтронов равномерно распределены в объеме активной зоны.
Далее, используя уравнения диффузии для тепловых нейтронов, запишем уравнения диффузии для замедляющихся нейтронов. Изменение концентрации нейтронов в активном объеме будет определяться только диффузией.
Концентрация замедляющихся нейтронов в единице объема: n1(r, t), r = (x, y, z)
∂n1(r,t)/∂t = DΔФ = DvΔn1(r,t)
Перейдем к функции плотности замедления: n1(r, t) = n2(r,E)⋅dE/dt = q (r, E).
Δq(r,τ) = ∂q(r,E) (ξE∑S)/(D∂E) = ∂q(r,τ)/∂τ — уравнение возраста нейтронов
Коэффициент размножения для бесконечной среды k∞ = vaεϕθ. В ограниченном объеме происходят утечки, поэтому вводят эффективный коэффициент размножения: kэф = ωk ω — вероятность избежать утечки из активной зоны (показывает, сколько нейтронов поглотилось в активной зоне). ω<1 всегда, тогда k∞>1, чтобы обеспечить нормальную работу реактора. k∞ характеризует потенциальную возможность осуществления цепной реакции. Если k∞≤1, то обеспечить самоподдерживающуюся цепную реакцию невозможно. k∞ определяется свойствами размножающей среды (составом). Уменьшая размер активной зоны мы можем снижать ω и создавать условия kэф = 1 — критическое состояние реактора. ω зависит от формы активной зоны, характера распределения полей замедляющихся и тепловых нейтронов в активной зоне.
Таким образом, появляется две задачи:
• Определить k∞
• Найти подходящую ω (геометрию и распределение полей), чтобы kэф = 1. Эту задачу можно решить, если мы будем знать распределение полей.