Конгруенции и фактор-алгебры, теоремы о гомоморфизме
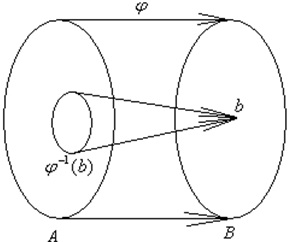
Пусть φ: A→B есть функция и φ(A)=B. Отображение φ: A→B порождает разбиение множества А на классы, ядерная эквивалентность, для которого σφ обладает тем свойствам, что a1σφa2↔φ(a1)=φ(a2) ∀a1, a2∈A. Пусть A/σ = {Ab; b∈B} есть множество классов эквивалентности (фактор- множество по эквивалентности σ), тогда отображение h: A/σ → B взаимнооднозначно, тогда отображение p:A → A/σ с p(a) = Aφ(a) есть каноническое отображение. Тогда φ = h*p есть каноническое представление функции φ. Пусть [a]σ есть класс эквивалентности, содержащий элемент a из A, тогда p(a)=[a]σ=Aφ(a), h([a]σ) = φ(a). Пусть записи (a,a’)∈σ, aσa’, a~a'(σ), a~a’ означают, что элементы a и a’ эквивалентны.
Определение: Функция fn из An → A сохраняет n – арное отношение ρ⊆Am, определенное на множестве A, если для ∀n наборов
(a11,…,a1m) ∈ρ
(a21,…,a2m)∈ρ
…
(an1,…,anm)∈ρ
(где столбец (a11,…,an1)=a1 и т.д. для других столбцов) набор (f(a1), …, f(an))∈ρ.
Замечание: Функция fp: An→A сохраняет отношение эквивалентности σ, определенное на A, если для ∀-эквивалентностей a1~a1‘, a2~a2‘, …, an~an‘ будет: f(a1, …, an) ~ f(a1‘,..,an‘).
И потому [f(a1,..,an)]σ=[f(a’1,..,a’n)]σ.
Определение: Эквивалентность σ, определенная на множестве A универсальной алгебры UA называется устойчивой эквивалентностью на UA, если всякая функция из ΩA сохраняет отношение σ. Пусть устойчивая эквивалентность σ задана на алгебре UA = (A, ΩA = {fini: i = 1,2,…}) . Пусть есть n- местная функция fn∈ΩA, определим A/σ одного типа с UA алгебру UA/σ = (A/σ, ΩA/σ = {Fini: i=1,2,…}) положим F([a1]σ,..,an]σ) = [f(a1,..,an)] ∀Fn∈ΩA/σ соответствующей операции fn∈ΩA.
Определение: Алгебра UA/σ называется фактор – алгеброй алгебры UA по устойчивой эквивалентности σ.
Теорема (основная о гомоморфизмах): Каноническое отображение p: A→A/ σ с p(a)=[a]σ алгебры UA в фактор – алгебру UA/σ есть гомоморфизм, для которого устойчивая эквивалентность σ есть ядерная эквивалентность.
Замечание: Множество всех гомоморфных образов алгебры UA имеет мощность множества всех устойчивых эквивалентностей σ, определенных на UA и потому множество гомоморфумных образов алгебры UA в алгебру UB с точностью до изоморфизма исчерпывается множеством всех фактор – алгебр алгебры UA по различным устойчивым эквивалентностям.