Ядерная тормозная способность

Длина пробега внедренных в пластину ионов определяется согласно теории Линдхарда, Шарфа и Шиотта. Механизмы потерь энергии иона при его торможении в мишени по этой теории предполагаются независимыми друг от друга и аддитивными. К двум важнейшим механизмам ионного торможения относятся упругие соударения ионов с ядрами атомов мишени и взаимодействие со связанными электронами мишени, что в обоих случаях приводит к их рассеянию. При торможении ионов потери энергии на единицу длины их пробега в мишени определяются выражением

dE/dx=N*(S_n+S_e) (1)

где Е—энергия иона; х—глубина его проникновения;
N—концентрация атомов в мишени; S_n,S_e —ядерная и электронная тормозные способности мишени.

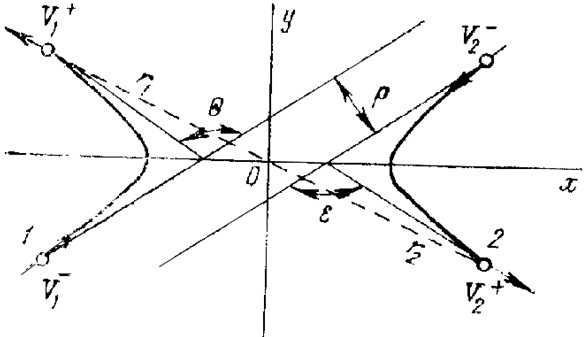
Рис.1. Схема рассеяния иона 1 и атома мишени 2 в системе центра масс

Рассмотрим задачу о рассеянии двух частиц, одна из которых до рассеяния покоится. Эта задача является частным случаем задачи для двух тел, когда интересуются лишь скоростями частиц после рассеяния (рис. 1). При соударении имплантируемый ион отклоняется от направления первоначального своего движения на угол θ и передает энергию атому мишени Е₁. Угол рассеяния может изменяться от 0 до 180°, причем значение θ=0 соответствует бесконечно далекому пролету иона, а θ= 180°—лобовому удару, значение Е₁ при этом меняется от 0 до

E_max = 4m₁m₂E/(m_m+m₂) (2)

где m₁ и m₂—относительные молекулярные массы иона примеси и атома мишени; Е — начальная энергия внедренного иона.

Расчеты показывают, что энергия E₁ зависит от угла рассеяния следующим образом:

E₁ = E_max/2 (1-cos θ) (3)

где угол θ является углом рассеяния частиц в системе центра масс (рис. 1). Зависимость угла θ от величины прицельного расстояния и скорости иона до рассеяния определяется интегралом

θ = π-2∫P/r² dr/[1-2U(r)/Eμ — P²/r²]^1/2 (4)

где U(r) — потенциал взаимодействия частиц; μ= m₂/(m₁ + m₂) -приведенная масса; r = r₁ + r₂ — расстояние между частицами в системе центра масс.

Потенциал взаимодействия частиц обычно принимается близким к кулоновскому

U(r) =z₁z₂q²/r f(r/a) (5)

где z₁ и z₂ — кратность зарядов ионов луча и мишени; q — заряд; а—параметр экранирования; f(r/a)—функция, учитывающая экранирование ядер электронными оболочками.

Важной характеристикой процесса рассеяния является дифференциальное эффективное поперечное сечение рассеяния. Для пучка падающих ионов эта величина определяется как отношение числа ионов, рассеянных в телесный угол dΩ за единицу времени, к числу ионов, пролегающих за единицу времени через единичную площадку поперечного сечения пучки до рассеяния.

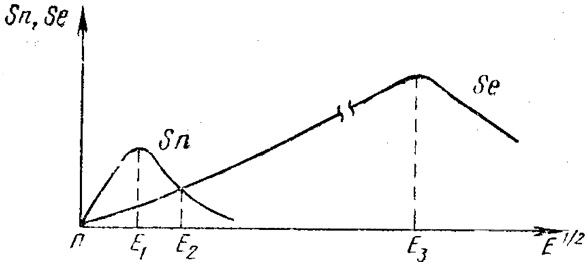
Рис.2. Зависимости электронной S_e и ядерной S_n тормозных способностей от энергии внедряемых ионов

Быстрые ионы имеют меньшее поперечное сечение. При средних значениях энергии ионов потери энергии за счет ядерного торможения увеличиваются, а для низких значений энергии ионов эти потери за счет эффекта экранирования электронными оболочками кулоновского заряда мишени вновь уменьшаются (рис. 2).

Электронная тормозная способность

Замедление ионов в мишени, согласно теории электронного торможения, пропорционально скорости или, что равнозначно, корню квадратному из их энергии
S_e = K√E
где К — коэффициент пропорциональности. Для некоторых используемых при ионной имплантации ионов на рис. 3 представлены расчетные зависимости потерь энергии, обусловленные ядерным и электронным торможением.

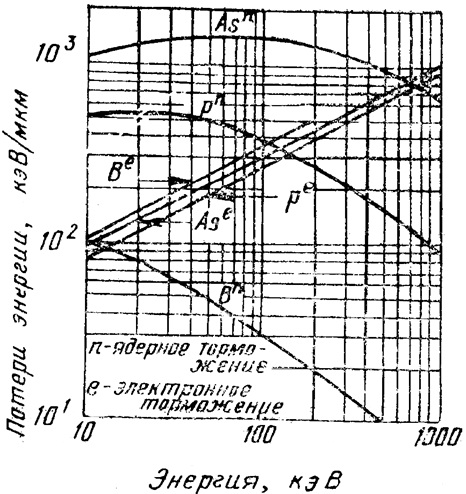
Рис.3. Расчетные зависимости тормозной способности (dE/dx) от энергии для As, P и В

Распределение пробегов ионов

В первом приближении распределение внедренных ионов по глубине мишени подчиняется гауссовой функции
N(x) = n(R_p)exp[-(x-R₂)²/2ΔR_p²]

где R_p — длина проекции общей траектории движения иона (рис. 4); ΔR_p—среднеквадратичное отклонение или рассеяние распределения. Максимальная концентрация n(R_p) на глубине R_p непосредственно связана с дозой имплантации D и может быть представлена в следующем виде:
n(R_p) = D/√(2π)ΔR_p

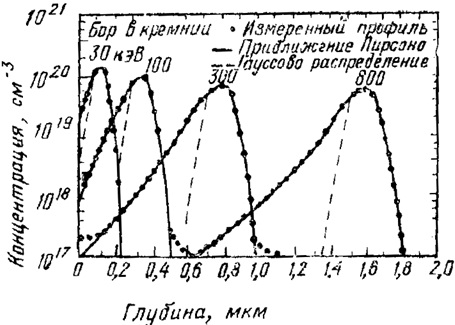
Рис.5. Экспериментальные и расчетные (с использованием модели Пирсона, учитывающей несимметричность реальных примесных слоев) распределения профилей имплантированных атомов бора

В ряде случаев экспериментальные кривые профиля распределения примеси при ионной имплантации описываются законом распределения, состоящим из двух наложенных гауссовых распределений, каждое из которых имеет свое собственное значение рассеяния ΔR_p1 и ΔR_p2. Более точнoe описание закона распределения требует использования большего числа эмпирических параметров и представляет основной интерес для определения профиля концентрации в технологии ионной имплантации.

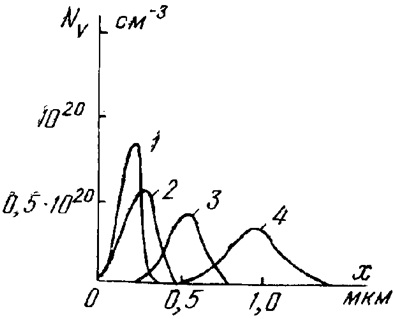
Рис.6. Распределение пробегов ионов бора различной энергии в кремнии: 1—Е= 50кэВ; 2—E=100кэВ; 3—E==200кэВ; 4—E=400кэВ

Значения средних пробегов R и их среднеквадратичных отклонений ΔR для ряда используемых в технологии ионной имплантации ионов представлены на рис. 6. Как следует из рис. 6, с увеличением глубины проникновения ионов происходит уменьшение максимальной концентрации ионов легированного слоя и рассредоточение внедренных ионов в мишени.

Влияние радиационных дефектов

Внедрение ионов в мишень приводит к образованию радиационных дефектов. Природа радиационных дефектов кристаллической решетки сложна и зависит от многих факторов таких, как кристаллографическая ориентация, температура мишени, размер и масса внедренных ионов. Легкие и тяжелые ионы производят качественно различные изменения в материале подложки. Легкие ионы в большей степени испытывают электронное торможение. После их замедления ядерное торможение начинает превалировать над электронным. В отличие от легких ионов тяжелые ионы начинают рассеиваться на первых атомных слоях мишени. В этом случае рассеянию подвергаются в значительной степенями атомы мишени. Плотность радиационных дефектов в обоих случаях повторяет распределение длин пробегов выбитых «из узлов кристаллической решетки атомов кремния (рис. 7).

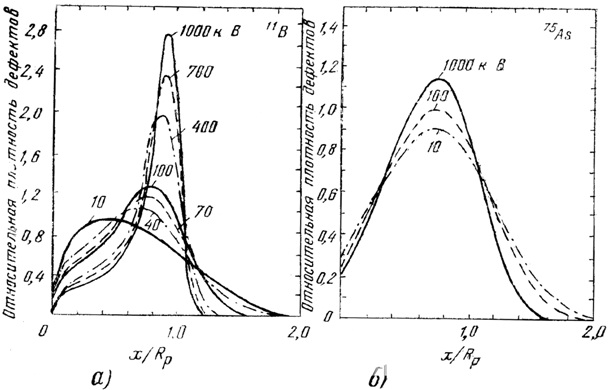
Рис.7. Расчетные профили распределения плотности введенных ионной имплантацией дефектов а—бора; б—мышьяка

Следует отметить, что при некоторой энергии бомбардирующих ионов, называемой критической, происходит переход монокристаллической пластины в аморфное состояние, что и определяет основную сложность получения легированных слоев глубиной более 1мкм. Увеличить глубину легирования при необходимости можно методом высокотемпературной диффузии. Диффузия имплантированных примесей протекает в условиях наличия помимо обычных дефектов комплексов вакансий и линейных дефектов, которые действуют в качестве стоков примесных частиц.

Ионное каналированние

В результате взаимодействия ионного пучка с атомами твердого тела происходят отклонение ионных траекторий от первоначального падения за счет упругого рассеяния на большие углы и потери энергии за счет неупругого рассеяния.

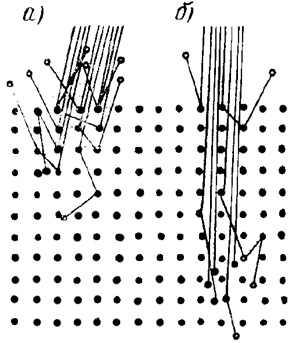
Рис.8. Модель эффекта каналирования ионов: а—сильное взаимодействие ионов у поверхности; б — ионы проникают в кристалл, проходя между рядами атомов вдоль каналов

В кристаллическом твердом теле периодичность структуры может оказать влияние на то, как происходит взаимодействие ионов с атомами кристаллической решетки. В частности, рассмотрим эффект каналирования ионов, который упрощенно показан на рис. 9. Эффект каналирования ионов возникает из-за различия в плотности упаковки атомов вдоль различных кристаллографических направлений. Так, если ионный пучок падает таким образом, как это показано на рис. 9, а, то в этом направлении плотность упаковки атомов велика и взаимодействие ионов преимущественно происходит вблизи поверхности мишени.

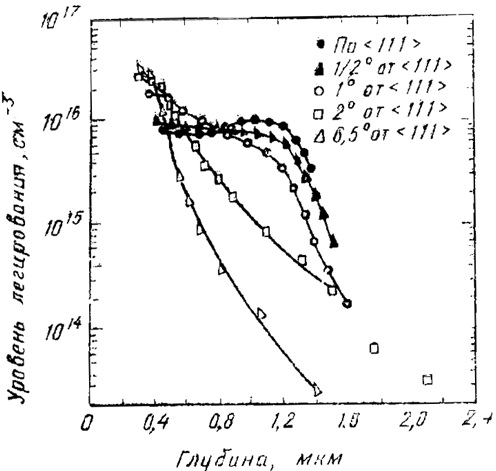
Рис.9. Профили распределения концентрации свободных носителей заряда для различной разориентации пластины от кристаллографического направления (111) (для ионов фосфора с энергией 300 кэВ и дозе облучения Д=10¹² ион см^-2)

Если пучок падает под несколько отличным от этого направления углом по отношению к кристаллу, то ионы проникают более глубоко в кристалл, проходя между рядами атомов вдоль «каналов», претерпевая с ними слабые скользящие столкновения.

Ориентация кремниевой пластины в наиболее плотно упакованных направлениях позволяет свести к минимуму эффект ионного каналирования, но не исключает его полностью. В тоже время использование эффекта каналирования позволяет проводить ионное легирование на большие глубины (рис. 9). Однако даже небольшие отклонения от требуемой ориентации ионного пучка относительно выбранного кристал-лографического направления приводят к плохой воспроизводимости результатов и к получению нескольких типов профилей распределения примеси. В результате соударения ионов с атомами кристаллической решетки мишени образуется аморфный слой с распределением 1′ внедренных в кристалл ионов, падающих в острофокусированном пучке и падающих на кристалл ионов под произвольным углом 1 (рис. 10).

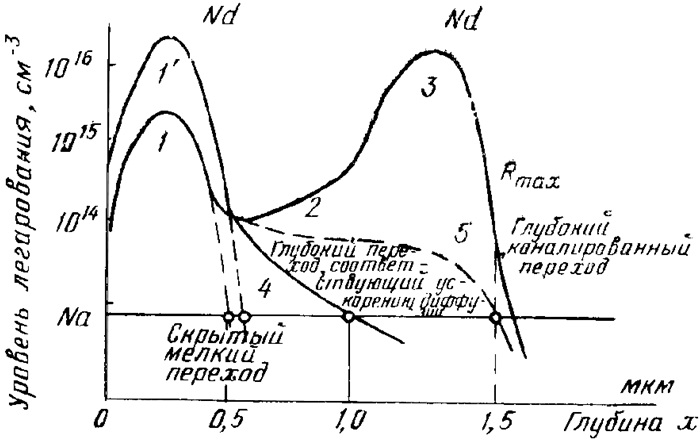
Рис.10. Разновидности профилей распределения примесей: 1— аморфный материал, входящий ионный пучок проникает в мишень под произвольными углами; 2— слабо ориентированный кристалл, деканалированный ионный пучок; 3—каналированнын ионный пучок, хорошо ориентированный кристалл; 4 — профиль, полученный при диффузии ионов примеси при отжиге; 5—эффект каналирования при незначительном отклонении ионного пучка относительно кристаллографической оси

Комментарии запрещены.