Метод заключается в том, что ионы, движущиеся в газовой среде, например, во внешней зоне коронного разряда, и сталкивающиеся с частицей, осаждаются на ее поверхности. Обратно ионы не могут возвратиться из-за того, что они должны обладать определенной энергией для преодоления потенциального барьера на границе раздела сред. Таким образом происходит накопление ионов на частице.

Рассмотрим зарядку частицы в электрическом поле с униполярным объемным зарядом. Увеличение заряда частицы определяется количеством ионов, попадающих на частицу в единицу времени:

dq/dt = e∫fdS (1)

где q — заряд частицы; e — заряд электрона; f — вектор плотности потока ионов; s — площадь поверхности частицы, на которую осаждаются ионы.

Поток ионов на частицу определятся движением ионов под действием электрического поля и движением, вызванным диффузией ионов за счет градиента концентрации ионов:

f = nkE — D grad n (2)

где E — напряженность электрического поля у поверхности частицы; n, k — концентрация и подвижность ионов; D — коэффициент диффузии.

Определим, при каких условиях преобладает зарядка частица за счет осаждения ионов под действием электрического поля («ударная» зарядка) и когда преобладает движение ионов под действием диффузионного механизма («диффузионная» зарядка). Из выражения (5.2.) следует, что «диффузионный» механизм преобладает над «ударным» при условии, если D grad n >> nkE. Предполагая, что у поверхности частицы n = 0, а ее возмущающее воздействие на концентрацию ионов распространяется на расстояние равное 2а, получаем grad n~n₀/2a. При атмосферном давлении в соответствии с молекулярно-кинетической теорией газов D ~ 0,025 k. Поэтому можно записать E << 0,025/(2a). Для условий, наблюдаемых в аппаратах электронно-ионной технологии, когда Е ~ (1-3) кВ/см, получаем, что при размерах частиц 2а << 0,1 мкм преобладает «диффузионный» механизм зарядки частиц. «Ударная» зарядка преобладает в этих условиях для частиц размером 2а >> 1 мкм.

«Ударная» зарядка частиц в электрическом поле
Результирующая напряженность поля у поверхности частицы определяется следующими составляющими: внешним полем Е_вн, полем поляризации частицы Е_п, полем заряда ионов, осевших на частицу, Е_q, полем зеркального отображения иона в поверхности частицы Е_з:

E = Е_вн + Е_п + Е_q + Е_з (3)

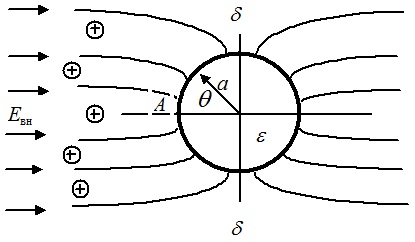
Рис.1. Схема ударной зарядки сферической частицы

Для сферической частицы (рис. 1) радиусом а и относительной диэлектрической проницаемостью ε в воздухе нормальная составляющая внешнего поля с учетом поля поляризации частицы (положительное направление — к частице) равна:

Е_вн + Е_пп = Е_внcosΘ + 2(ε-1)/(ε+2) Е_внcosΘ = Е_внk_ε cosΘ (4)

где Θ — меридиональный угол сферической системы координат, k_ε = 1 + 2(ε-1)/(ε+2) = 3ε/(ε+2) — коэффициент, учитывающий относительную диэлектрическую проницаемость частицы.

Напряженность кулоновского поля от заряда частицы, отталкивающего подлетающие ионы, равна

E_q = -q / (4πε₀a²) (5)

Поле зеркального отображения иона действует на малом расстоянии от поверхности частицы, и его можно учесть как увеличение эффективного радиуса частицы, поскольку все ионы, попавшие в пределы зоны действия силы зеркального отображения, захватываются частицей. Для рассматриваемых размеров частиц этим увеличением можно пренебречь.

Подставляя значения напряженностей электрического поля в выражения (2) и (1), получим:

dq/dt = ek∫nk_εE_внcosθ (-q/4πε₀a²) (6)

Численные расчеты показывают, что концентрация ионов при движении в электрическом поле в указанных условиях не изменяется вдоль траектории движения ионов. Если на достаточном удалении от частицы эта концентрация равна n₀, то она n₀ и вдоль поверхности частицы. Следовательно, она может быть вынесена за знак интеграла в формуле (6).

Интегрирование в (6) производится в сферической системе координат по той части поверхности частицы, где поле обеспечивает попадание иона на частицу. Следовательно:

dq/dt = en₀k/(4ε₀q_m)[q(t) — q_m]² (7)

где q_m = 4πε₀a²E_вн — максимальный заряд частицы.

Очевидно, что в самом начале зарядки частицы (q = 0) ионы осаждаются на всей левой половине частицы (граница δ-δ). По мере накопления заряда на частице, благодаря усилению отталкивающего поля область осаждения ионов сокращается (граница δ-δ) смещается влево) вплоть до нуля (граница δ-δ) проходит через точку А). В этом случае зарядка частицы прекращается и частица приобретает максимальный заряд.

Решением дифференциального уравнения (7) является выражение (формула Потенье):

q(t) = q_m en₀kt/(4ε₀ + en₀kt) (8)

Для проводящей частицы можно считать, что ε→∞ и k_ε = 3. Тогда:

q_m = 12πε₀a²E_вн (9)

При зарядке частицы в биполярной короне, когда в пространстве, окружающем частицу, наряду с ионами одного знака (например, положительными — n₊, k₊) присутствуют ионы другого знака (отрицательные — n_—, k_—), поток зарядов на частицу имеет две составляющие: положительную, увеличивающую заряд частицы, и отрицательную, уменьшающую ее заряд.

Предельный заряд в этом случае равен:

q_пред = q_m [1 — √(en_—k_—/en₊k₊)] / [1 + √(en_—k_—/en₊k₊)] (10)

где γ_v+ = en₊k+ и γ_v- = en_—k_— — проводимости, определяемые соответственно положительными и отрицательными зарядами. Из формулы (10) видно, что предельный заряд, приобретаемый частицей в поле биполярного коронного разряда, меньше максимального заряда частицы, получаемого при униполярной зарядке q_пред < q_m.

«Диффузионная» зарядка частиц
Для малых частиц (2а << 0,1 мкм) поток ионов на частицу определяется только процессом диффузии, а из электрических сил необходимо учитывать лишь отталкивающее воздействие приобретаемого заряда частицы. Тогда общий поток ионов на частицу будет равен:

Ф = ∫D(dn/dr — kn q/4πε₀a²)ds (11)

За положительное направление принято направление потока к центру частицы. Подстановка в (1) и интегрирование уравнения дает решение в неявном виде:

t = ε₀/(en₀k) [E_i(A) — c₀ — ln A] (12)

где E_i — интегральная показательная функция; А = kq/(D 4πε₀a); c₀=0,577 — постоянная Эйлера.

Определив величину А из (12) легко можно найти заряд q.

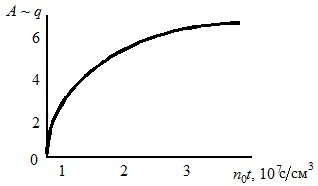
Зависимость параметра А от времени зарядки и концентрации ионов

При диффузионном механизме зарядки заряд растет во времени неограниченно. Объясняется это тем, что по мере накопления заряда на частице и роста его отталкивающего действия растет градиент концентрации ионов у поверхности частицы за счет сосредоточения изменения концентрации все в более узком слое вблизи поверхности частицы. Однако график (рисунок выше) показывает, что основной заряд частица приобретает в начальный период времени (n₀t ≤ 2×10₇ с/см³), а далее он изменяется мало. За предельный заряд принимается А_пред= 6,7 при n₀t = 4×10⁷с/см³.

Строго аналитического решения задачи при одновременном учете «ударного» и «диффузионного» механизмов зарядки нет и задача решается численно. В результате численных расчетов установлено, что при 0,1 ≤ а ≤ 1 мкм величину заряда можно вычислять как сумму зарядов, рассчитанных по формулам «ударной» и «диффузионной» зарядки.

Если форма частиц существенно отличается от сферической, то используется замена частицы на частицу эллипсоидальной формы эквивалентную по соотношению осей и объема. Следует иметь в виду, что если форма частицы близка к сферической, то она при зарядке вращается. Частицы удлиненной формы в электрическом поле приобретают определенную ориентацию, и это обстоятельство следует учитывать при расчете величины заряда. Формулы для «ударной» и «диффузионной» зарядки эллипсоидов можно найти в соответствующей литературе.

Комментарии запрещены.