Теорема 1. (теорема Ляпунова об устойчивости) Если для уравнений возмущенного движения (1.18) можно найти знакоопределенную функцию V, производная V^• которой в силу этих уравнений была бы или знакопостоянной функцией противоположного знака с V, или тождественно равной нулю, то невозмущенное движение x=0 устойчиво относительно величин x₁, x₂, …, x_N.

Геометрическая интерпретация теоремы 1. Пусть для определенности найдена положительно-определенная функция V(x), производная которой в силу уравнений (1.18)
либо V^•(x) постоянно-отрицательная, либо V(x)≡0 тождественно равна нулю (если V(x) отрицательно-определенная функция, то можно взять функцию (-V), которая будет
положительно-определенной функцией).

Покажем, что изображающая точка М, начав движение в сфере B_δ, никогда не выйдет на сферу B_ε.

В окрестности начала координат возьмем сферу (рис.3.8)
B_ε: ∑x_i²=ε²,
а внутри нее поверхность V = c. По заданному числу ε выберем число δ так, чтобы сфера
B_δ: ∑x_i²=δ²
лежала внутри поверхности V = c и не имела с ней общих точек.

Пусть изображающая точка М начала движение при t = t₀ из точки М₀(x₀), лежащей внутри сферы B_δ.

Выберем поверхность V = c₀, которая проходит через начальную точку М₀. Поскольку точка М₀ лежит внутри поверхности B_δ (и, естественно, внутри поверхности V = c), то c₀< c и поверхность V = c₀ лежит внутри поверхности V = c.

При своем дальнейшем движении при t > t₀ точка М будет либо входить внутрь поверхности V = c₀ в случае V^• < 0, так как cos α < 0, либо будет находиться на ней в случае V^• = 0, так как cos α = 0. Во внешнюю часть поверхности V = c₀, т.е. вне сферы B_ε, точка М не сможет перейти.

Следовательно, невозмущенное движение системы (1.18) устойчиво по Ляпунову относительно величин x₁, x₂, …, x_N.

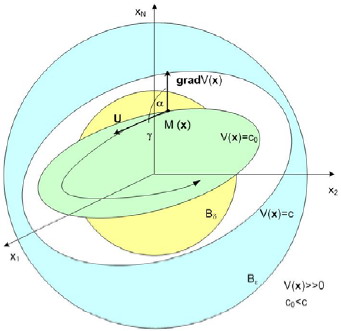
Рис.3.8 Геометрическая интерпретация теоремы Ляпунова об устойчивости

Пример 1. Исследовать устойчивость нулевого решения системы
x^• = — x + 3y², y^• = — 3xy,
В качестве функции Ляпунова взять V = x² + y².

Пример 2. Исследовать устойчивость нулевого решения системы x^• = — x + 3y², y^• = — xy — y³,
В качестве функции Ляпунова взять V = x² + y².

Теорема 2. (теорема Ляпунова об асимптотической устойчивости) Если для уравнений возмущенного движения (1.18) можно найти знакоопределенную функцию V, производная V^•, которой в силу этих уравнений была бы знакоопределенной функцией противоположного знака с V, то невозмущенное движение x = 0 асимптотически устойчиво относительно величин x₁, x₂, …, x_N.

Геометрическая интерпретация теоремы 2.
В этом случае изображающая точка М, начавшая движение при t = t₀ на поверхности V = c₀ при t > t₀ войдет внутрь этой поверхности. Далее она будет пересекать все поверхности V = c_k (k=1,2,…,m,…), где 0<...k<...< c₂10 (лежащие внутри поверхности V = c₀), снаружи внутрь так, что при t→∞ точка М будет стремиться к началу координат (к невозмущенному движению x = 0).

Следовательно, невозмущенное движение системы (1.18) асимптотически устойчиво по Ляпунову относительно величин x₁, x₂, …, x_N.

Пример 3. Исследовать устойчивость нулевого решения системы x^• = — x + 3y², y^• = — 3xy — y,

В качестве функции Ляпунова взять V = x² + y².

Пример 4. Исследовать устойчивость нулевого решения системы x^• = — x + 3y², y^• = — 3xy — y³.

В качестве функции Ляпунова взять V = x² + y².

Теорема 3. (теорема Ляпунова о неустойчивости) Если для уравнений возмущенного движения (1.18) можно найти функцию V такую, что ее производная V^• в силу этих уравнений была бы знакоопределенной функцией, а сама функция V могла бы принимать в окрестности x = 0 значения одного знака со своей производной V^•, то невозмущенное движение x = 0 неустойчиво относительно величин x₁, x₂, …, x_N.

Обобщением теоремы Ляпунова о неустойчивости является следующая теорема.

Теорема 4. (теорема Четаева о неустойчивости) Если для уравнений возмущенного движения (1.18) можно найти функцию V такую, что в сколь угодно малой окрестности x = 0
существует область V > 0, и если производная V^• в силу этих уравнений положительна во всех точках области V > 0, то невозмущенное движение x = 0 неустойчиво относительно величин x₁, x₂, …, x_N.

Замечание 4. Если V положительно-определенная функция, то областью V > 0 является вся окрестность нуля. Геометрическая интерпретация теоремы 4. Для доказательства неустойчивости невозмущенного движения достаточно найти всего одну траекторию изображающей точки
М, которая выходит из сферы B_ε.

Пусть в начальный момент времени t = t₀ точки М находилась в области V>0. В этой области производная V^•>0, поэтому функция V монотонно возрастает, а точка М при t > t₀ не выйдет из этой области. Действительно, внутри области V>0 имеем cos α > 0, а на границе этой области (где V = 0) cos α = 0. Следовательно, траектория точки М никогда не выйдет на границу этой области. Она с течением времени будет уходить в сторону возрастания функции V и при некотором значении t = t₁ > t₀ выйдет из сферы B_δ. Следовательно,
невозмущенное движение x = 0 неустойчиво относительно величин x₁, x₂, …, x_N.

Пример 5. Исследовать устойчивость нулевого решения системы
x^• = x² + 2y³, y^• = xy².

В качестве функции Ляпунова взять V = x² — y⁴.
Показать с помощью теоремы Четаева, что
нулевое решение неустойчиво.

Приведенные теоремы Ляпунова дают достаточные условия устойчивости и неустойчивости невозмущенного движения относительно x.

Комментарии запрещены.