Определение (неустойчивости по Ляпунову) Невозмущенное движение q_p = ξ(t), q_p^•=ξ^•(t) системы (1.1) называется неустойчивым по Ляпунову относительно величин q, q^•, если существуют числа ε₁₀, ε₂₀ > 0 такие, что для любых чисел δ₁, δ₂ > 0 существует решение q(t), q^•(t) уравнений (1.1) и момент времени t₁ > t₀ такие, что,

хотя ||q(t₀) — ξ₀|| < δ₁, ||q^•(t₀) — ξ₀^•|| < δ₂, тем не менее ||q(t₁) — ξ(t₁)|| > ε₁₀, ||q^•(t₁) — ξ^•(t₁)|| > ε₂₀.

Геометрическая интерпретация определения неустойчивости по Ляпунову в фазовом пространстве q₁,…, q_n , q₁^•,…, q_n^•

На рис.1.3 представлена геометрическая интерпретация определения устойчивости по Ляпунову на фазовой плоскости q, q^• для случая системы с одной степенью свободы (n=1). Начав в начальный момент времени t=t₀ движение из точки М₀(q(t₀), q^•(t₀)), лежащей в B_δ-окрестности начальной точки ξ₀, ξ^•₀ невозмущенного движения ξ(t), ξ^•(t), где B_δ:
|q(t₀) — ξ₀|< δ₁, |q^•(t₀) — ξ^•₀| < δ₂, изображающая точка М через конечный интервал времени при t= t₁ выйдет из B_ε — окрестности данного невозмущенного движения, где B_ε: |q(t) — ξ(t)| < ε₁,
|q^•(t) — ξ^•(t)| < ε₂.

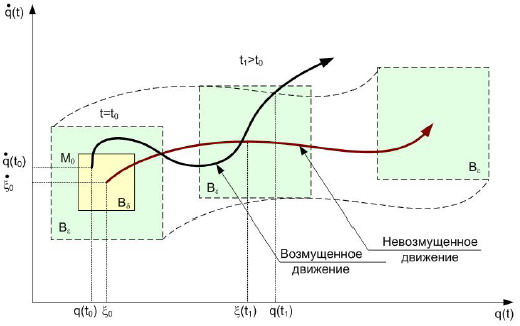
Рис.1.3 Геометрическая интерпретация определения неустойчивости по Ляпунову на фазовой плоскости

Определение (асимптотической устойчивости по Ляпунову): Невозмущенное движение _p=ξ(t), q_p^•=ξ^•(t) системы (1.1) называется асимптотически устойчивым по Ляпунову относительно величин q, q^•, если
а) оно устойчиво;
б) если существуют такие числа Δ₁, Δ₂ > 0, что для любых q(t₀), q^•(t₀), удовлетворяющих неравенствам
||q(t₀) — ξ₀|| < Δ₁, ||q^•(t₀) — ξ₀^•|| < Δ₂, выполняются условия
q(t) → ξ(t), q^•(t) → ξ^•(t) при t → ∞. (1.9)

Геометрическая интерпретация определения асимптотической устойчивости по Ляпунову в фазовом пространстве q₁,…, q_n , q₁^•,…, q_n^•

На рис.1.4 представлена геометрическая интерпретация асимптотической определения устойчивости по Ляпунову на фазовой плоскости q, q^• для случая системы с
одной степенью свободы (n=1). Начав при t=t₀ движение из точки М₀(q(t₀), q^•(t₀)), лежащей в B_δ-окрестности начальной точки ξ₀, ξ^•₀ невозмущенного движения ξ(t), ξ^•(t), где B_δ: | q(t₀) — ξ₀| < δ₁, |q^•(t₀) — ξ^•₀| < δ₂, изображающая точка М в случае асимптотической устойчивости невозмущенного движения ξ(t), ξ^•(t) при t ≥ t₀ не выйдет из B_ε-окрестности данного невозмущенного движения, где B_ε: |q(t) — ξ(t)|< ε₁, |q^•(t) — ξ^•(t)| < ε₂ и при t → ∞ будет неограниченно приближается к нему.

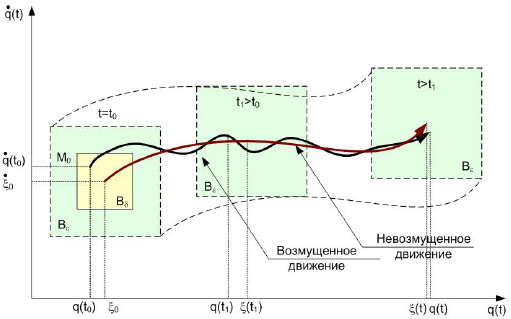
Рис.1.4 Геометрическая интерпретация определения асимптотической устойчивости по Ляпунову на фазовой плоскости

Комментарии запрещены.