Существуют различные критерии определения знака действительных частей корней характеристического уравнения (2.3). Наибольшее распространение получил критерий Рауса-Гурвица, который дает необходимые и достаточные условия отрицательности действительных частей всех корней характеристического уравнения системы.

Запишем характеристическое уравнение (2.3) в виде полинома

Δ(λ) = λ^N + a₁λ^N-1+ … + a_N-1λ + a_N = 0. (2.4)

Составим матрицу Гурвица

Заметим, что необходимым условием выполнения неравенств (2.6) является условия Стодолы – условия положительности всех коэффициентов характеристического полинома (2.4)
a_k > 0 (k = 1, 2, …, N).

Критерий Льенара-Шипара Для того чтобы корни алгебраического уравнения (2.4) с действительными коэффициентами a_k имели отрицательные действительные части, необходимо и достаточно, чтобы:

1. При N = 2m (четном) все коэффициенты характеристического полинома (2.4) и главные
диагональные миноры (2.5) матрицы Гурвица нечетного порядка были положительными
a₁ > 0, …, a_N > 0, Δ₁ > 0, Δ₃ > 0, Δ₅ > 0, …, Δ_2m-1 > 0.

2. При N = 2m+1 (нечетном) все коэффициенты характеристического полинома (2.4) и главные диагональные миноры (2.5) матрицы Гурвица четного порядка были положительными
a₁ > 0, …, a_N > 0, Δ₂ > 0, Δ₄ > 0, Δ₆ > 0, …, Δ_2m > 0.

Если уравнений движения (2.2) четное количество и уравнения «симметричны» относительно переменных и параметров системы, то бывает удобно осуществить операцию компрессии этих уравнений, перейдя к комплекснозначным переменным, например, z=x₁+ix₂ (смотри ниже пример 2.4).

Тогда для уравнений первого приближения, записанных в новых комплекснозначных переменных, характеристическое уравнение будет представлять собой алгебраическое уравнение (2.7)
Δ*(λ) = λ^N + a₁*λ^N-1+ … + a*_N-1λ + a_N* = 0, (2.7)
в котором коэффициенты a₁*, …, a_N* будут комплексными величинами.

Для исследования характеристического уравнения (2.7) удобно применить критерий Рауса-Гурвица II для полиномов с комплексными коэффициентами.

Преобразуем характеристическое уравнение (2.7), сделав в нем замену λ=iμ. В
результате получим преобразованное характеристическое уравнение следующего вида
(c₀ + ib₀) μ^N + (c₁ + ib₁) μ ^N-1 + … + (c_N-1 + ib_N-1) μ + (c_N + ib_N) = 0 (2.8)

Составим определители матрицы Гурвица для полинома (2.8)

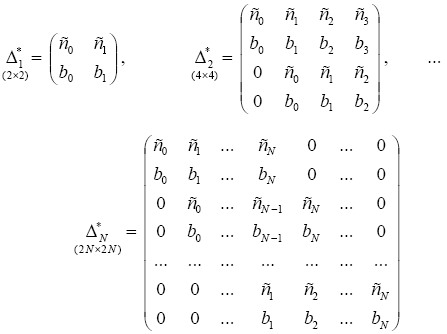
Критерий Рауса-Гурвица II (для полиномов с комплексными коэффициентами) Для того чтобы все корни μ_k (k = 1, … , N) алгебраического уравнения с комплексными коэффициентами (2.8) имели положительные мнимые части Im μ_k > 0 (это означает, что все
корни λ_k характеристического полинома (2.7) имеют отрицательные действительные части Re λ_k < 0), необходимо и достаточно, чтобы все определители Δ*k имели чередующиеся знаки, начиная с первого отрицательного (-1)k Δ*_k > 0 (k = 1, 2, …, N)

Обращение в ноль какого-либо коэффициента характеристического полинома (2.4) или главного диагонального минора (2.5) матрицы Гурвица приводит к невыполнению условий критериев Рауса-Гурвица или Льенара-Шипара и, соответственно, к невыполнению словий теоремы Ляпунова об устойчивости по первому приближению. В этом случае нулевое решение линейной системы (2.2) не является асимптотически устойчивым. Однако, тем не менее, оно может быть просто устойчивым (не асимптотически).

Для исследования устойчивости нулевого решения системы (2.2) в этих случаях необходимо применять другие методы, например, методы, основанные на анализе структуры сил, действующих на системе.

Комментарии запрещены.