Проведен анализ влияния амплитудно-фазовой анизотропии интерференционных зеркал на поляризационные характеристики кольцевого лазера (эллиптичность, сдвиги частот, потери). Определена комбинация параметров зеркала, при которой наблюдается максимальная чувствительность поляризационных характеристик к непланарной деформации осевого контура. Показано, что существует диапазон оптимальных значений фазовой анизотропии зеркал.

1. Введение

Кольцевые лазеры, используемые в лазерных гироскопах, обладают рядом особенностей: малое усиление активной среды, высокая степень монохроматичности, одномодовый и одночастотный режим генерации. Вследствие этого, к резонаторам кольцевых лазеров предъявляются жесткие требования: сверхмалые потери, стабильность параметров в широком диапазоне температур и к воздействию различных внешних факторов. Необходимо также контролировать и уменьшать ошибки изготовления и сборки оптических резонаторов.

Одним из видов ошибок является непланарная деформация осевого контура, которая возникает, если резонатор образован, естественно, более чем тремя вершинами осевого контура (вершина осевого контура – это точка, где осевой луч изменяет направление). Выведение осевого контура резонатора из одной плоскости иногда предпринимают специально, например, для формирования круговых собственных состояний поляризаций.

Поляризационные характеристики кольцевых лазеров существенно зависят от анизотропии отражателей, образующих непланарный оптический резонатор: интерференционных зеркал или призм полного внутреннего отражения. Цель настоящей работы состоит в определении оптимальной анизотропии интерференционных зеркал, которая позволяет обеспечить минимум потерь излучения и малую чувствительность характеристик четырехзеркального кольцевого лазера к магнитному полю при непланарной деформации осевого контура.

2. Методика расчета

В непланарных резонаторах плоскости падения-отражения осевого луча на соседних вершинах осевого контура не совпадают. Состояние поляризации волн определяется во вращающейся системе координат ξ_iη_iζ_i, ось ξ_i которой лежит в плоскости падения i-ой оптической поверхности. При пере-ходе в следующее плечо резонатора ось η_i поворачивается на угол кручения α_i вокруг продольной оси. Для встречной волны направление оси ζ_i меняется на противоположное, при этом система координат остается правой.

Методика анализа непланарных резонаторов состоит в следующем. Необходимо задать вид непланарной деформации осевого контура, рассчитать координаты вершин осевого контура и определить углы кручения между плоскостями падения осевого луча на каждую вершину. Затем следует составить циклический оператор Джонса с учетом вращателей, описывающих разворот последовательных плоскостей падения, и матриц амплитудно-фазовой анизотропии, характеризующей каждую вершину и плечо осевого контура, и, наконец, решить собственную задачу, т.е. определить собственные состояния поляризации, потери и сдвиги частот встречных волн.

Рассмотрим четырехзеркальный резонатор бегущей волны с деформированным квадратным осевым контуром KLMN (рис. 1), плечи которого имеют одинаковую длину a. Зеркала резонатора будем считать одинаковыми. Пусть исходный осевой контур KLMN деформируется по диагонали MOK, так что точка N выводится из плоскости исходного осевого контура на расстояние Δ. Угол излома диагонали LON равен γ = arcsin(√2Δ/a).

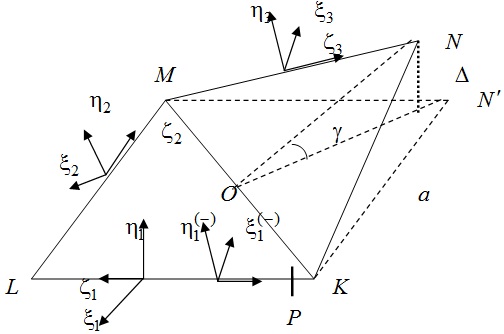
Рис. 1. Непланарный резонатор

Выберем расчетное сечение P вблизи зеркала K и станем обходить резонатор по часовой стрелке (PLMNKP). При обходе резонатора перед каждым зеркалом поворачиваем координатный базис ξ_iη_iζ_i вокруг осевого луча на некоторый угол кручения α. Это означает, что в каждом плече резонатора находится неполярный (естественный) вращатель с параметром α. Если угол γ мал, то угол кручения приближенно равен α ≈ ± √2γ/2

Для встречной волны ориентация осей координатного базиса отличается, как показано на рис. 1, где знак «–» означает, что данный базис относится к волне, обходящей резонатор против часовой стрелки.

Полный оператор Джонса находим как произведение матриц Джонса вращателей и отражателей

T₀ = T(α)T_MT(-α)T_MT(-α)T_M (1)

где

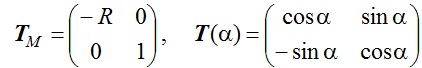
Здесь R = R_p/R_s = (1 — t) exp(iϕ) – коэффициент амплитудно-фазовой анизотропии зеркала; ϕ = ϕ_p — ϕ_s – разность сдвигов фаз ортогональных компонент вектора Е при отражении; t ≈ t_p — t_s ≈ (τ_p — τ_s)/2 – параметр относительной амплитудной анизотропии; τ_p, τ_s – энергетические коэффициенты пропускания. Для интерференционных зеркал t и дополнительный к 180° сдвиг фазы ϕ обычно являются малыми величинами.

3. Результаты расчета

В случае резонатора, образованного зеркалами, более добротной (с меньшими потерями) является s-мода, вектор Е которой перпендикулярен плоскости падения на каждое зеркало. Как следует из расчетов по описанной выше методике, дополнительные поляризационные потери A_s, обусловленные непланарностью, и поляризационная переменная Г_s = E_x/E_y равны

A_s ≈ 8Re(1-R)/(1+R)α², Г_s ≈ ± α/(1+R) (2)

В четырехзеркальном непланарном резонаторе (см. рис. 1) состояние поляризации излучения, как правило, становится эллиптическим и изменяется после отражения от каждого зеркала. Во всех плечах резонатора направление вращения вектора Е – противоположное для встречных волн (это означает, что в своих координатных базисах с противоположным направлением про-дольной оси встречные волны имеют одинаковые знаки углов эллиптичностей). Если на активную среду такого кольцевого лазера наложить магнитное поле, то возникает невзаимный сдвиг частот встречных волн.

Рассмотрим влияние параметров зеркала на поляризационные характеристики кольцевого лазера, для которых важным является соотношение час-тот и потерь встречных добротных мод.

В случае интерференционных зеркал параметры их анизотропии зависят от числа слоев N, отношения λ/λ₀ (λ – длина волны падающего излучения, λ₀ – номинальное значение длины волны), от изменения угла падения и т.д. При отклонении λ/λ₀ от единицы линейно возрастает фазовая анизотропия ϕ, причем, если λ/λ₀ ≈ 1.02, то ϕ ≈ 5° (рис 2).

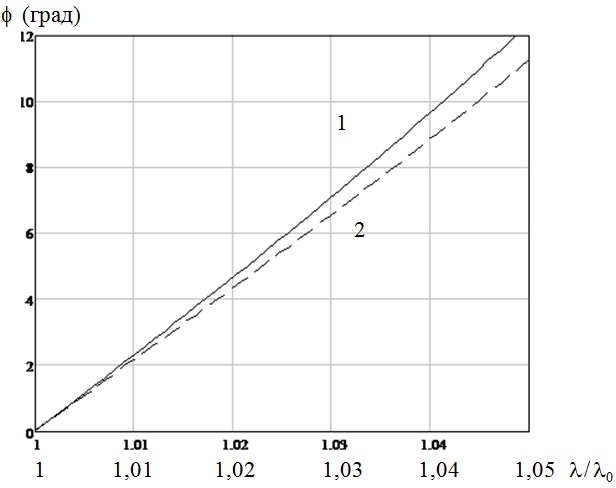
Рис. 2. Зависимость сдвига фаз между
ортогональными компонентами вектора напряженности от отношения длины волны света к номинальному значению длины волны для зеркала
(1: N=23, 2: N=13)

Амплитудная анизотропия в основном зависит от числа слоев зеркала: чем больше N, тем меньше t, например, при N=21: t ≈ 10^-3. При λ/λ₀ = 1.05 параметр t увеличивается примерно в полтора раза (рис. 3).

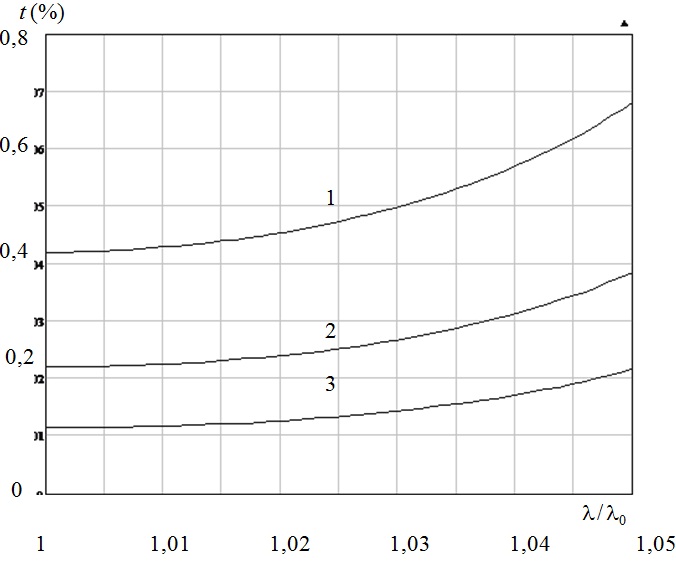
Рис. 3. Зависимость параметра относительной амплитудной анизотропии
от λ/λ₀ при различном значении N:
(1 – N = 17 ; 2 – N = 19 ; 3 – N = 21)

Проведенный анализ показывает, что существует комбинация параметров зеркала, при которой чувствительность поляризационных характеристик к непланарной деформации оказывается максимальной (при малых углах кручения):

ϕ₀ = t (3)

Этих значений параметров амплитудно-фазовой анизотропии зеркал следует избегать при их изготовлении. При выполнении (3) дополнительные потери A_max ≈ 4α²/ϕ₀ и угол эллиптичности χ_max ≈ α/2ϕ₀ достигают максимальных значений.

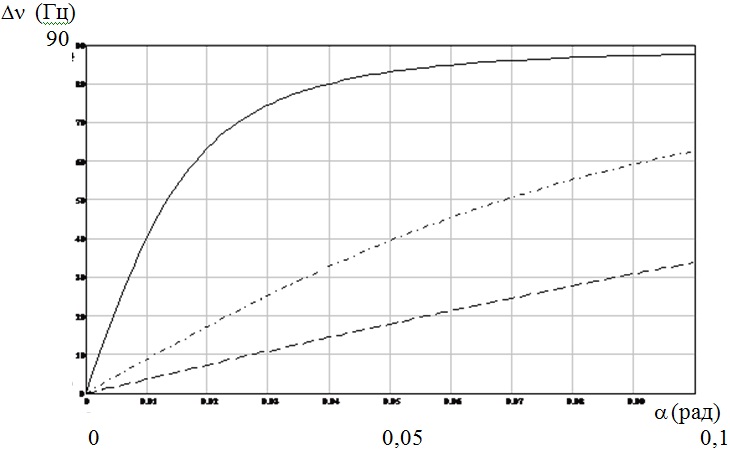
Рис. 4. Зависимость сдвига частот Δν встречных волн кольцевого лазера в магнитном поле при различном значении фазовой анизотропии зеркал
(сплошная линия – λ/λ₀ =1.01 ; штрих-пунктир – λ/λ₀=1.05; пунктир – λ/λ₀=1.1)

На рис. 4 показана расчетная зависимость сдвига частот встречных волн в магнитном поле от угла кручения α, при этом приняты следующие значения: параметр фарадеевского вращателя равен 0.26×10^-6, что примерно соответствует реальному значению усиления в активной среде кольцевого лазера, напряженность магнитного поля – 1 эрстед и периметр осевого контура – 0, 28 м.

0 при угле кручения α = 5×10^-5 и различном значении N» src=https://all4study.ru/img/raznoe/7.jpg>
Рис. 6. Зависимость угла эллиптичности χ (град) от λ/λ₀ при угле кручения α = 5×10^-5 и различном значении N:
(1 – N = 15 , 2 – N = 17 ; 3 – N = 19; 4 – N = 21)

На рис. 5, 6 показаны зависимости потерь и угла эллиптичности при различном соотношении параметров амплитудно-фазовой анизотропии зеркал, определяемой N и λ/λ₀. Из анализа рис. 4 – 6 следует, что для уменьшения чувствительности поляризационных характеристик к непланарной деформации осевого контура необходимо увеличивать фазовую анизотропию зеркал до 10°, при этом λ/λ₀ ≈ 1.04.

4. Выводы

1. Амплитудно-фазовая анизотропия интерференционных зеркал оказывает существенное влияние на потери, угол эллиптичности и сдвиги частот встречных волн кольцевого лазера с непланарным резонатором.

2. При определенном соотношении параметров амплитудной и фазовой анизотропии зеркал возрастает чувствительность поляризационных характеристик кольцевого лазера к непланарной деформации осевого контура резонатора.

3. Для уменьшения влияния непланарной деформации осевого контура на поляризационные характеристики следует обеспечивать оптимальный диапазон значений фазовой анизотропии зеркал: 5°< ϕ < 10°, изменяя параметры интерференционного покрытия (количество слоев, их толщину и показатель преломления).

Комментарии запрещены.