Сформулируем теперь условия оптимальности для задачи условной оптимизации (1.32).

Предположим, что ограничения g_i (х) являются непрерывными дифференцируемыми функциями и уравнения связи g_i(х) =b_i, i = 1,2,…, m < n, могут быть разрешены относительно части переменных (не нарушая общности будем считать, что зависимыми переменными являются m первых компонент x₁, х₂,…, х_n). Для того чтобы выполнялось последнее условие, необходимо, чтобы ранг матрицы Якоби для функций g_i (х), i = 1, 2,…, m, равнялся m, т. е. определитель этой матрицы, составленной из производных по первым m аргументам, не равнялся нулю:

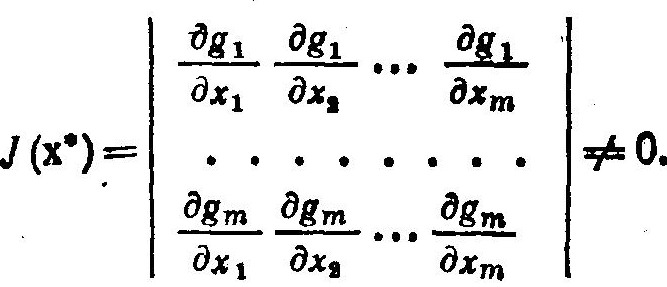
Для того чтобы точка х* ∈ D являлась оптимальным решением задачи условной оптимизации (1.32), она должна удовлетворять системе из (n + m) уравнений вида:

∂Q/∂x_j|_x=x* + ∑λ_k∂g_k/∂x_j|_x=x* = 0, j=1, 2, …, n;

g_i (x*) = b_i, i = 1, 2, …, m. (1.60)

По теореме о неявных функциях, если в точке х* выполняется условие (1.59), то из уравнений связи g_i (х) = b_i, i = 1, 2, …, m, можно выразить зависимые переменные через независимые!

x_i = φ_i (x_m+1, x_m+2, …, _n), i = 1, 2, …, m (1.61)

где φ_i (x_m+1, x_m+2, …, _n) — непрерывные дифференцируемые функции. Подставляя (1.61) в функцию Q (х), получаем для любых значений х ∈ d (х*, ε) следующее выражение:

Q (φ₁(x_m+1, x_m+2, …, _n), …. φ₁(x_m+1, x_m+2, …, _n), x_m+1, x_m+2, …, _n = Q* (x_m+1, x_m+2, …, _n). (1.62)

Точка х* является локальным минимумом функции Q* (x_m+1, x_m+2, …, _n). если выполняется условия оптимальности (1.55) для многопараметрической задачи безусловной оптимизации:

∂Q*/∂x_j |_x=x* = 0, j = m+1, m+2, …, n. (1.63)

По правилу дифференцирования сложных функций, учитывая (1,62), вместо (1.63) можем записать:

∂Q*/∂x_j |_x=x* = ∑∂Q*/∂x_i ∂φ_i/ ∂x_j + ∂Q*/∂x_j =0, j = m+1, …, n, (1.64)

где производные ∂φ_i/ ∂x_j, i — 1, 2, …, m, для каждого j представляют собой единственное решение системы уравнений;

∑∂g*/∂x_i ∂φ_i/∂x_j + ∂g*/∂x_j = 0, k = m+1, …, n,

Вместо того чтобы решать систему уравнений (1.65), поступим следующим образом. Рассмотрим совокупность чисел λ_i, i = 1, 2, …, m, являющихся решениями системы линейных уравнений:

∑λ_i∂g_i/∂x_j + ∂Q/∂x_j =0, j = 1, …, m, (1.66)

Решение системы (1.66) существует и единственно в силу предположения (1.59). Умножим k-ое уравнение (1.65) на λ_k и просуммируем по k от 1 до m. Тогда для каждого j = m + 1, …, n, если поменять порядок суммирования, справедливо соотношение

∑ ( ∑ λ_i ∂g_i/∂x_j)∂φ_i∂x_j + ∑λ_i ∂g_i/∂x_j = 0.

Прибавляя (1.67) к (1.64), имеем:

∑[ ∂Q/∂x_i + ∑λ_i ∂g_i/∂x_j]∂φ_i/∂x_j + [ ∂Q/∂x_j + ∑λ_i ∂g_i/∂x_j] = 0

откуда, учитывая (1.66), получаем, что для выполнения соотношений (1.63), необходимо, чтобы выполнялась система уравнений:

∂Q/∂x_j + ∑λ_i ∂g_i/∂x_j = 0, j=m + 1,…, n. (1.69)

Объединяя эту систему с системой уравнений (1.66) и уравнениями связи g_i (х) — b_i, i = 1, …, m, получаем, что точка х* является оптимальным решением задачи условной оптимизации (1.32), если она удовлетворяет системе (n+m) уравнений (1.60).

Условия оптимальности (1.60) для задачи условной оптимизации (1.32) могут быть получены при помощи следующего приема, называемого методом множителей Лагранжа.

Составляется функция (n + m) переменных х = (х₁, х₂,…, х_n) и λ = (λ₁, λ₂,…, λ_n), которые считаются независимыми:

L(x, λ) = Q(x) + ∑λ_i(g_i(x) — b_i),

по каждой из компонент векторов х и λ, вычисляются частные производные от функции L (х, λ) и приравниваются нулю:

∂L/∂x_j = ∂Q/∂x_j + ∑λ_i ∂g_i/∂x_j, j = 1, 2, …, m;

∂L/∂λ_i = g_i(x) — b_i, i = 1,2,…, n.

Функция L (х, λ) называется функцией Лагранжа, а числа λ_i, которые могут иметь любой знак, множителями Лагранжа.

Представляет интерес ответить на вопрос: какова в терминологии рассматриваемой задачи оптимизации (1.32) интерпретация искусственно введенных множителей Лагранжа λ_i, i = 1, 2,…, m. С этой целью рассмотрим поведение минимального значения критерия оптимальности Q* = Q (х*) при изменении правых частей b_i, i = 1, …, m, уравнений связи:

g_i (х) = b_i, i = 1, 2, …, m. (4.70)

Пусть х* — оптимальное решение задачи условной оптимизации (1.32), а λ*— множители Лагранжа, соответствующие точке х*. Очевидно, что х* и λ* являются функциями правых частей уравнений связи (1.70):

х* = х* (b), λ* = λ* (b). (1.71)

Предположим, что зависимости (1.71) являются непрерывно дифференцируемыми функциями вектора b = (b₁, b₂,…, b_n), и вычислим частные производные критерия оптимальности Q (х*) и уравнений связи (1.70) по b_i в точке х*:

∂Q/∂b_i|_x=x* = ∑∂Q/∂x_j∂x_j/∂b_i, j = 1, 2, …, m; (1.72)

∂g_k/∂b_i|_x=x* = ∑∂g_k/∂x_j∂x_j/∂b_i — δ_ik, i, k = 1, 2, …, m; (1.73)

где

δ_ik = 1, если i=k
0 — в противном случае.

Умножим k-e уравнение (1.73) на λ*_k, просуммируем по k от 1 до m и прибавим его к правой части выражения (1.72). Тогда, меняя порядок суммирования, можем записать

∂Q/∂b_i = ∑(∂Q/∂x_j + ∑λ*_k∂g_k/∂x_j)∂x_j/∂b_i — ∑λ*_kδ_ik, i = 1, 2, …, m.

Так как х* и λ* удовлетворяют условиям оптимальности (1.60), то, учитывая (1.74), получим, что

∂Q/∂b_i | _x=x* = — λ*_i, i = 1, 2, …, m.

Таким образом, множители Лагранжа λ*_i, i = 1, 2, …, m, можно интерпретировать как коэффициенты чувствительности минимального значения критерия оптимальности Q (х*) к малым изменениям правых частей уравнений связи (1.70).

Практическое значение полученного результата заключается в том, что, не решая задачи оптимизации (1.32) при новых значениях правых частей уравнений связи (1.70), мы можем оценить, как изменится оптимальное значение критерия оптимальности при малых изменениях вектора b.

При выводе условий оптимальности для задачи выпуклого программирования (1.30) необходимо допустить, что выпуклая допустимая область D имеет внутренние точки. Наличие таких точек гарантирует, что существует хотя бы одна точка х ∈ D, в которой все ограничения могут быть разделены на два типа: активные ограничения, в которых неравенства выполняются как равенства (g_i (х) = b_i i ∈ J^—), и неактивные ограничения, являющиеся строгими неравенствами (g_k (х) > 0, k ∈ J⁺, J⁺ ≠ ∅). Существование внутренних точек множества D можно определить также следующим образом.

Будем называть направление S возможным направлением в точке х ∈ D если можно двигаться вдоль направления S, оставаясь в D. Область D имеет внутренние точки, если возможное направление S в точке х для любого активного ограничения удовлетворяет следующим условиям, называемым условиями регулярности:

(∇g_i^T(x), S) ≥ 0, i∈J^—. (1.75).

Пусть допустимая область D = {x|g_i(x) ≥ 0, i = 1, 2, …, m} удовлетворяет условиям регулярности (1.75). Тогда для того, чтобы точка х* ∈ D была оптимальным решением задачи выпуклого программирования (1.30), необходимо существование таких чисел u* = (u₁*, u₂*,…, u_m*), что

g_i(x*) ≥ 0, i = 1, 2, … m; (1.76)
u_i* ≥ 0, i = 1, 2,…, m; (1.77)
u_i*g_i(х*) = 0, i = 1, 2, …, m; (1.78)

∇Q(x*) — ∑u_i*∇g_i(x*) = 0.

Комментарии запрещены.