Обобщая полученный результат (1.52) на многомерный случай, для задачи (1.29) безусловной минимизации многопараметричеекой унимодальной функции Q (х) можем сформулировать следующие условия оптимальности.

Для того чтобы точка х*∈Rⁿ являлась оптимальным решением (локальным минимумом) необходимо и достаточно, чтобы в этой точке градиент минимизируемой функции равнялся нулю, а ее гессиан был положительно определенной матрицей:
∇Q(x*) = grad Q(x*) = 0 или

∂Q/∂x_j, j = 1,2,…, n; (1.55)
x^TG(x*)x > 0 для любых х ≠ 0. (1.56)

Для задачи (1.28) многопараметрической минимизации унимодальной функции Q (х), определенной в n-мерном параллелепипеде D_x = {x|x_j^—≤x_j≤x_j^—, j=1, 2, …, n}, условия оптимальности формулируются следующим образом.

Для того чтобы точка х*∈D_x являлась оптимальным решением (локальным минимумом), необходимо, чтобы выполнялись следующие условия:

∂Q/∂x_i|_x=x* > 0, если х_i* =x_i^—;

∂Q/∂x_i|_x=x* < 0, если х_i* =x_i⁺;

∂Q/∂x_i|_x=x* = 0, если x_i^— < x_i* < x_i⁺;

Доказательство справедливости условий (1.57) проведем для одной переменной x_i*, предположив, что остальные (n — 1) переменные остаются неизменными.

Пусть точка х* является точкой локального минимума функции Q (х). Тогда для любой точки (x_i* + ξ) ∈d (х*, ξ) справедливо неравенство

Q(x_i*+ξ) ≥ Q(x_i*),

или, используя формулу Тейлора (1.54), получаем, что

Q(x_i*+ξ) — Q(x_i*) ≈ ξ dQ/dx_i|_x=x* ≥ 0. (1.58)

Пусть х_i* =x_i^—. При этом возможны только положительные значения приращения ξ > 0 (рис. 1.10, кривая Q₁ (x)), т. е. для выполнения неравенства (1.58) необходимо, чтобы первая производная функции Q (х) по переменной x_i; была положительна dQ/dx_i > 0. Аналогично, при х_i* =x_i⁺, возможны только отрицательные значения приращения ξ < 0 (рис. 1.10, кривая Q₂ (x)), т. е. для выполнения неравенства (1.58) необходимо, чтобы первая производная функции Q (х) по переменной х_i была отрицательной: dQ/dx_i < 0. Если x_i^— < x_i < x_i⁺, то приращение

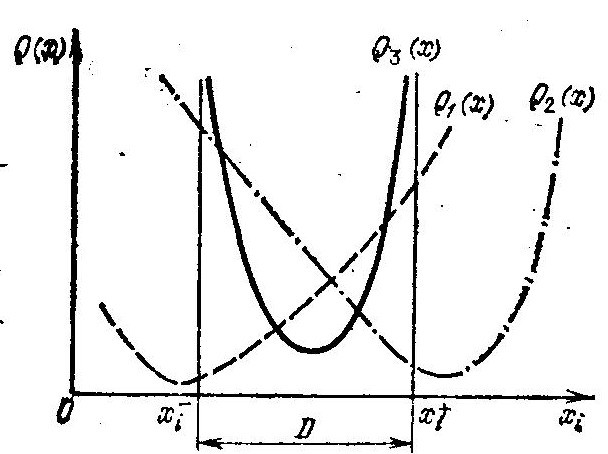
Рис. 1.10. Условия оптимальности унимодальной функции, определенной на отрезке [x_i^—, x_i⁺]

ξ может быть любого знака (рис. 1.10, кривая Q₃(x)), т. е. выполнение неравенства (1.58) возможно только при равенстве нулю первой производной функции Q (х) по переменной x_i:

dQ/dx_i = 0

Условия оптимальности (1.57) показывают, что оптимальное решение х* задачи многопараметрической оптимизации (1.28) может находиться как внутри области D_x, так и на границе гиперпараллелепипеда, т. е. одна или несколько его координат могут принять предельные значения (x_i^— или x_i⁺). Наличие такой ситуации требует для отыскания оптимального решения х* применения следующей процедуры. Сначала решается задача безусловной оптимизации для функции Q (х). Затем решается 2n задач безусловной оптимизации для функций Q_i от (n — 1)-й переменной, которые получаются из Q (х) подстановкой x_i = x_i^— или x_i = x_i⁺. После этого рассматривается Зn (n — 1) задач безусловной оптимизации для функций Q_ij от (n — 2)-х переменных, которые получаются из Q (х) путем подстановки вместо x_i и x_j всевозможных сочетаний их предельных значений и т. д. Оптимальное решение х* задачи (1.28) будет совпадать с наименьшим из минимумов всех рассмотренных задач безусловной оптимизации. Очевидно, что такой подход к решению задачи оптимизации (1.28) требует больших вычислительных затрат. Поэтому в некоторых специальных случаях целесообразно применять функции преобразования x_i = f_i (z), рассмотренные ранее, для того чтобы перейти от исходной задачи (1.28) к задаче безусловной оптимизации (1.31).

Комментарии запрещены.