При решении задачи оптимального проектирования часто приходится иметь дело с математическими моделями, в которых не имеется аналитических выражений для первых производных минимизируемой функции Q(х). В связи с чем поиск оптимального решения х* приходится вести по результатам вычислений функции Q (х). Методы, которые используют для выбора точки очередного испытания х^r информацию только о значениях функции Q (х), называются методами прямого поиска (методами нулевого порядка, методами минимизации без вычисления производных).

Наиболее простыми из алгоритмов данного класса методов являются алгоритмы, реализующие метод покоординатного спуска. Основная идея этого метода заключается в том, что поиск точки минимума х* сводится к поочередному изменению переменных вдоль одной из координатных осей:

x_i^r+1 = x_i^r + λ_i^rI_i, i = 1,2, …, n. (5.94)

где I_i — i-й координатный n-мерный вектор с компонентами:

l_ij = 1, если i = j;
l_ij = 0 — в противном случае.

Длина шага λ_i^r вдоль направления поиска I_i может выбираться равной некоторой постоянной величине Δ_i по следующему правилу:

λ_i^r = Δ_i, если Q(x^r + Δ_iI_i) < Q(x^r);
λ_i^r = -Δ_i, если Q(x^r — Δ_iI_i) < Q(x^r) < Q(x^r + Δ_iI_i). (5.95)

Если окажется, что λ_i^r = 0 для всех i = 1, 2, …, n, то длина пробных шагов Δ_i должна быть уменьшена (Δ_i = Δ_i/β, где β > 1). Поиск считается законченным при выполнении условия:

max Δ_i < ε. (5.96)

Алгоритм F²⁹, реализующий описанную стратегию поиска точки минимума x*, называется методом покоординатного спуска с постоянным шагом.

Когда длина шага λ_i^r на каждой итерации определяется с помощью одномерной задачи оптимизации

Q(x^r + λ_i^rI_i) = min Q(x^r + ∑λ_k^rI_k + λ_iI_i) (5.97)

приходим к алгоритму F³⁰, реализующему релаксационный метод Гаусса — Зейделя, процедура поиска точки минимума X* в котором сводится к следующей последовательности действий.

1. Задается начальное приближение х^r = х°.
2. Осуществляется циклический покоординатный спуск из точки
х^r по формуле (5.94) с выбором длины шага λ_k^r, из условия (5.97) для
всех i от 1 до n. Эта процедура образует внутренний цикл, в процессе которого осуществляется одномерная минимизация функции Q (х) по каждой переменной:

min Q(х₁^r, …, х_i-1^r, x_i, х_i+1^r, …, х_n^r), i = 1, 2, …, n.

3. После окончания внутреннего цикла в качестве начального приближения х° принимается точка хⁿ и все вычисления повторяются с п. 2.

4. Поиск точки минимума х* заканчивается, если после очередного внутреннего цикла выполняется условие

||х^r — хⁿ|| < ε.

Геометрической интерпретацией траектории поиска, которая получается по алгоритмам F²⁹ и F³⁰ является ломаная, состоящая из отрезков прямых, параллельных осям координат.

Недостатком методов покоординатного спуска (алгоритмы F²⁹ и F³⁰) является то, что при минимизации функций, имеющих овраг, дно которого не ориентировано вдоль какой-то из координатных осей, процесс поиска сильно замедляется и может остановиться далеко от точки истинного минимума x*.

В связи с этим рассмотрим алгоритм F³¹, реализующий метод конфигураций, который позволяет осуществлять поиск вдоль произвольно ориентированного относительно координатных осей дна оврага.

Процесс поиска начинается из начального приближения х°, которое принимается за базовую точку х^r, характеризующуюся тем, что она является исходной точкой очередной итерации. Каждая итерация состоит из двух процедур: «пробного движения» в Δ-окрестности текущей точки испытания и «движения в допустимом направлении», т. е. в направлении вдоль которого гарантируется уменьшение функции Q (X).

Процедура «пробного движения» заключается в обследовании Δ-окрестности базовой точки х^r с целью определения допустимого (удачного в смысле уменьшения функции Q (х)) направления S^r. Для этого в циклическом порядке, начиная с i = 1, по формуле (5.94) изменяется каждая переменная x_i, i = 1,2, …, n, где размер шага вдоль координатного направления I_i выбирается из условия (5.95). При этом начальный размер шага Δ_i для каждой из переменных может иметь различные значения. Если полученное значение λ_i^r не равно нулю, то при выполнении пробного движения вдоль (i+1)-й координаты в качестве значения Q (х^r) рассматривается либо Q (х^r + Δ_iI_i) (если λ_i^r = Δ_i), либо Q (х^r — Δ_iI_i) (если λ_i^r = — Δ_i). После просмотри всех координатных направлений I_i получается точка x_n^r, в которой значение функции Q (х_n^r) меньше или равно значению функции в баз вой точке Q (х^r). Если окажется, что х_n^r = х^r т. е. величина принятого пробного шага Δ настолько велика, что не позволяет определить допустимого направления, то необходимо его уменьшить (Δ_i = Δ_i/β, β > 1) и повторить пробные движения снова. Таким образом, пс мере приближения к точке минимума х* длина пробного шага Δ уменьшается. Поиск считается законченным, если размер всех пробных шагов Δ_i, i = 1, 2, …, n, станет меньше заданной точности ε.

В случае выполнения неравенства

Q (x_n^r) < Q (х^r)

в качестве допустимого направления S^r выбирается вектор (x_n^r — х^r), который указывает направление поиска вдоль дна оврага минимизируемой функции. Периодическое повторение пробных движений позволяет подстраивать траекторию поиска вдоль дна оврага.в тех случаях, когда (вследствие криволинейности оврага) установленное на предыдущей r-й итерации допустимое направление S^r оказывается неудачным для (r + 1)-й итерации.

Процедура «движения в заданном направлении» сводится к следующей последовательности действий. Вдоль направления определяется по формуле

x_i^r+1 = x^r + h(x_n^r — x^r), (5.98)

где h > 1 шаг вдоль допустимого направления.

После каждого шага i = 1, 2,…, вдоль допустимого направления относительно точки х_i^r+1 проводится процедура «пробного движения», целью которой является определение, не нуждается ли направление S в коррекции. Если полученная после проведения n пробных движений точка x_in^r+1 не совпадает с точкой х_i^r+1, то в качестве скорректированного допустимого направления выбирается вектор (х_in^r+1 — х_i^r+1), вдоль которого делается шаг h > 1:

х_i+1^r+1 = х_i^r + h(х_in^r+1 — х_i^r+1), (5.98)

где x_i^r+1 — «удачная точка» вдоль допустимого направления S^r. Если точка х_in^r лежит на одной прямой с точками х^r и х_n^r, то направление S^r сохраняется (не корректируется). В обоих случаях вычисление функции Q (х) вдоль допустимого направления продолжается до тех пор, пока в очередных точках испытания х_i+1^r+1 получаются уменьшающиеся значения функции Q (х). Когда в допустимом направлении не удается найти точку испытания x_i+1^r+1 с меньшим значением функции Q (х), то поиск в направлении S^r считается законченным. В этом случае точка предыдущего удачного испытания x_i^r+1 выбирается в качестве базовой точки для (r+1)-й итерации, из которой делается пробное движение с целью определения нового допустимого направления S^r+1.

На рис. 5.3 показана траектория поиска, реализующая пробные движения и движения в допустимом направлении для функции Q (x₁, x₂) «овражного» типа.

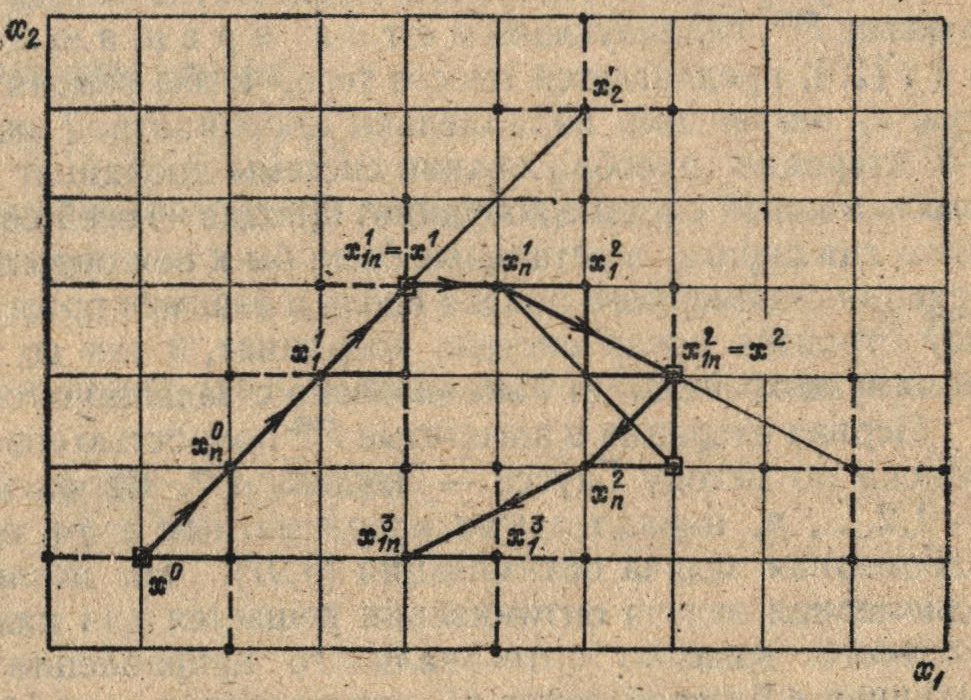
Рис. 5.3. Траектория поиска по методу конфигураций минимума функции Q(x) с «криволинейным» оврагом

Применение алгоритма F³¹оказывается эффективным при минимизации функций Q (х) с «прямолинейными оврагами». В этом случае экспериментально показано, что число испытаний, необходимое для локализации точки минимума х* с заданной точностью ε, прямо пропорционально числу переменных n.

Недостатком алгоритма является то, что в процессе проведения пробных движений направление дна оврага может быть пропущено, так как пробные шаги делаются только параллельно координатным осям. По этой же причине поиск может «остановиться» на дне оврага вдали от точки истинного минимума х*, если в базовой точке линии уровня минимизируемой функции (Q (х) = const) очень изогнуты.

Для устранения отмеченного недостатка метода конфигураций в алгоритме F³², реализующем метод вращающихся координат, предлагается вместо того, чтобы изменять каждую переменную x_i независимо параллельно координатной оси, осуществлять на r-й итерации преобразование системы координат (х) таким образом, чтобы в новой системе координат (ξ) одна из осей совпадала с направлением дна оврага, а остальные были бы к ней ортогональны. После проведения одномерного поиска вдоль n взаимно ортогональных направлений строится новая система координат, и так до тех пор, пока точка минимума X* не будет локализована с заданной точностью ε.

Первая итерация в алгоритме F³² полностью совпадает с процедурой поиска по методу Гаусса — Зейделя F³⁰. Вдоль направлений I_i, i = 1,2, …, n, параллельных координатным осям, поочередно решается одномерная задача оптимизации (5.97). На последующих итерациях одномерная задача оптимизации решается для каждого линейно-независимого взаимно ортогонального направления ξ_i, i = 1, 2, …, n. Начиная с базовой точки х^r, определяется шаг λ₁^r вдоль направления ξ₁^r, при котором достигается min Q (х^r + λ₁ξ₁^r).

Комментарии запрещены.