Метод поиска, реализующий процедуру выбора точек испытаний по формулам (3.8)—(3.9) (см. предыдущий пост) коэффициентами t_k*, которые вычисляются из выражений (3.37), называется методом Фибоначчи. Это название возникло в связи с тем, что стратегия поиска оптимального решения х* по данному методу, как нетрудно видеть, связана с использованием чисел Фибоначчи (3.29).

На первом этапе, который соответствует первому шагу поиска (k = 0), эквидистантно от концов априорного интервала неопределенности [a, b] проводится пара испытаний в точках, определяемых N-м и (N — 1)-м числами Фибоначчи:

x₁¹ = а + (b — a) U_N-1/u_N+1; (3.38)
x₂¹ = а + (b — a) U_N/u_N+1;

Согласно условию унимодальности функций Q (х) перед вторым этапом происходит сокращение интервала неопределенности по информации о ее значениях в точках x₁¹ и x₂¹: если Q (x₁¹) < Q (x₂¹), то a₁ = а и b₁ = x₂¹, в противном случае а₁ = x₁¹ и b₁ = b.

Второй этап поиска включает в себя (N — 3) итерационных шага k = 1, 2, …, N — 3, на каждом из которых в интервале неопределенности [а_k, b_k] рассматривается пара испытаний, расположение которой задается следующими формулами:

x₁^k+1 = a_k + (b_k— a_k)u_N-k-1/u_N-k+1, (3.39)

x₂^k+1 = a_k + (b_k— a_k)u_N-k/u_N-k+1. (3.40)

При проведении испытаний по формулам (3.39)— (3.40) на каждом шаге второго этапа (k = 1, 2, …, N — 3) необходимо заново вычислять только одну координату для точки нового испытания (x₁^k+1 иди x₂^k+1).

Пусть на k-м шаге имеем Q (x₁^k) < Q (x₂^k). Из условия унимодальности функции Q (х) на (k + 1)-м шаге будет исследоваться уже интервал [a_k+1, b_k+1], где a_k+1 = a_k, b_k+1 = х₂^k, внутри которого находится точка x₁^k. На (k + 1)-м шаге из выражения (3.40) можем записать

x₂^k+1 = a_k+1 + (b_k+1 — a_k+1)u_N-k/u_N+1-k = a_k + (x₂^k — a_k)u_N-k/u_N-k+1.

Подставим в полученное выражение значение x₂^k из (3.40):

x₁^k+1 = a_k + (b_k — a_k) u_N-k-1/u_N-k+1.

Откуда, учитывая (3.39), получаем, что

x₁^k+1 = x₁^k.

Что и требовалось показать. Аналогично доказывается, что при Q (x₁^k) ≥ Q(x₂^k) имеем x₁^k+1 = x₂^k.

После проведения (N — 1)-го испытания необходимо решить, по какую сторону от точки x₁^N-3 (x₁^N-3), находящейся внутри интервала, неопределенности [а_N-2, b_N-2], лежит точка истинного минимума х*.

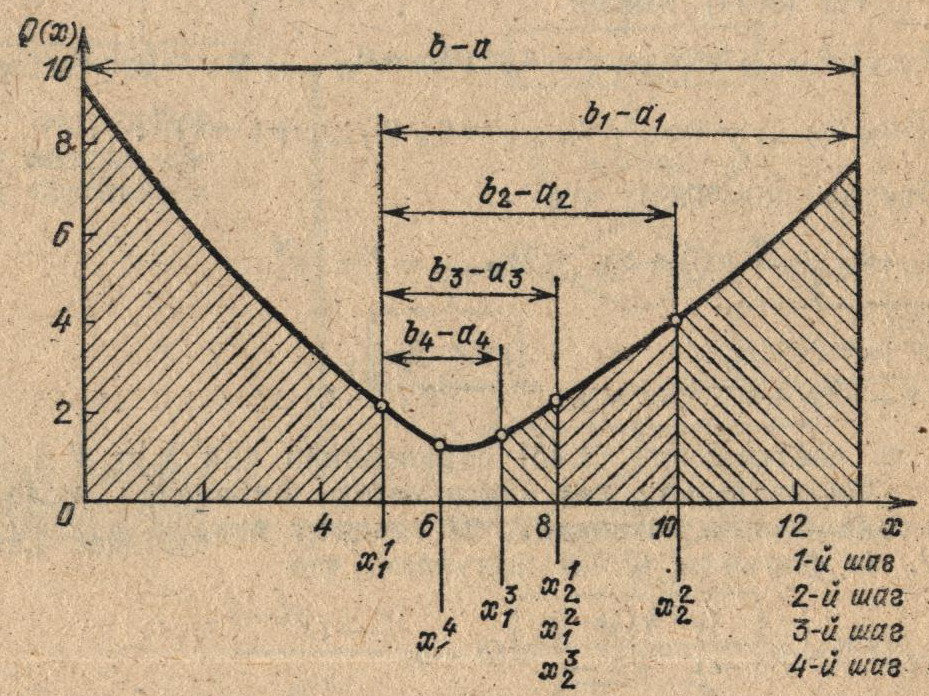
Рис. 3.2. Первые четыре шага поиска минимума унимодальной функции по методу Фибоначчи

Для этого последнее N-e испытание проводится вблизи от точки предыдущего испытания в точке (x₁^N-3 — δ), что позволяет Определить апостериорный интервал неопределенности [a_N, b_N]. Этим заканчивается третий этап поиска по методу Фибоначчи.

Для нечетного числа испытаний N длина апостериорного интервала неопределенности, получаемого с помощью метода Фибоначчи, равна:

l_N (F²) = (b — a)/u_N. (3.41)

Подставляя оптимальнее решение t₀ из (3.36) в (3.34), для апостериорного интервала неопределенности при нечетном числе испытаний N можем записать:

b_N — a_N = (b-a)(u_N+1u_N+2 — u_Nu_N-1)/(u_N+1)

На рис. 3.3 показана зависимость отношения длин апостериорных интервалов неопределенности методов поиска F¹ и F¹ от допустимого числа испытаний N:

l_N (F¹)/l_N (F²) = u_N/2^N/2.

Из приведенной зависимости видно, что метод Фибоначчи F² на классе унимодальных функций является более эффективным, чем метод деления пополам F¹. Так, например, при N = 14 апостериорный интервал неопределенности, полученный по методу F², приблизительно в 5 раз меньше апостериорного интервала неопределенности, гарантированного методом F¹.

Недостаток метода Фибоначчи заключается в том, что в нем априори необходимо задавать число испытаний N, так как на первом этапе поиска требуется вычислять N-oe и (N — 1)-ое числа Фибоначчи для определения параметра t₀. В связи о этим рассмотрим экстремальную задачу (3.15)—(3.17), но введем при этом дополнительное требование о том, что на каждой итерации коэффициенты t_k сохраняют постоянное значение t*:

t_k = t* = const, k = 0, 1, 2, …, N — 1.

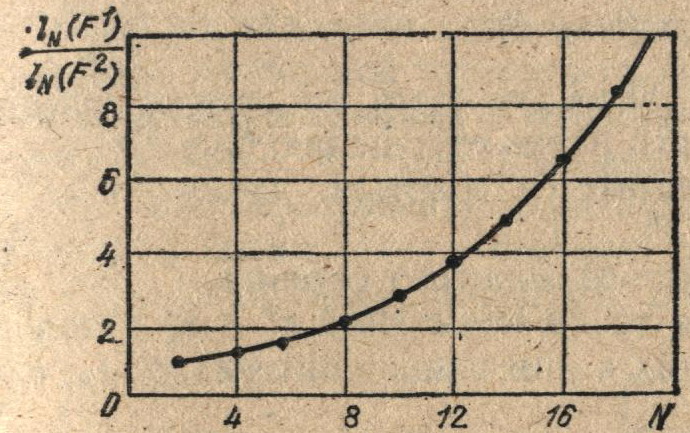
Рис. 3.3. Зависимость отношения критериев эффективности метода деления пополам и метода Фибоначчи от числа испытаний N

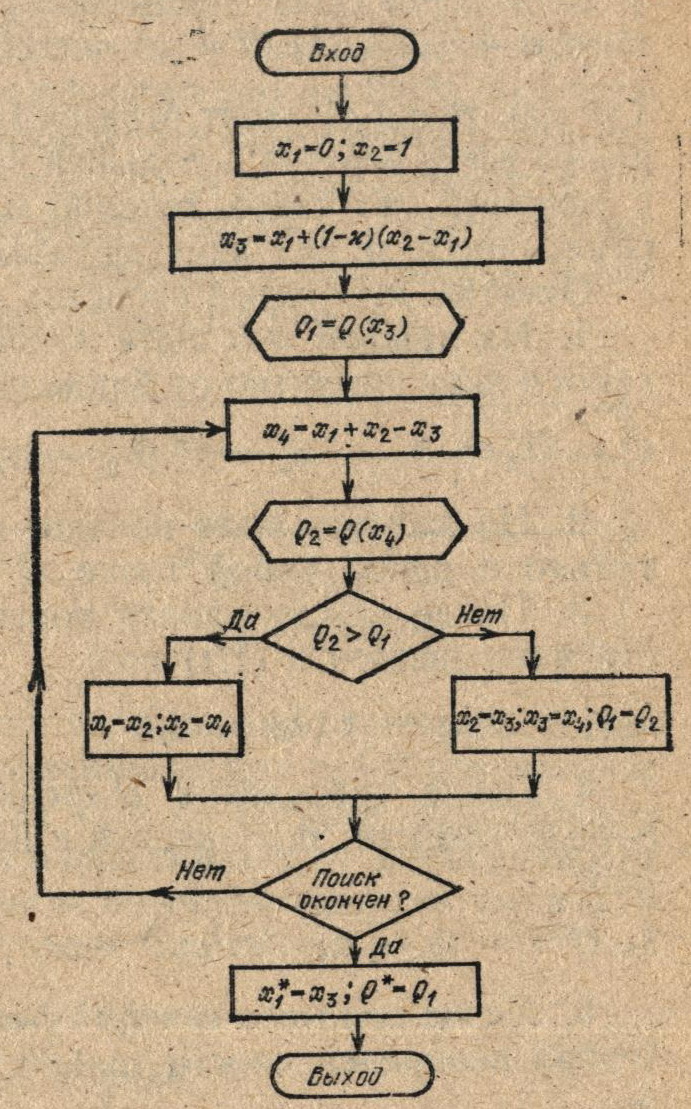
Рис. 3.4. Блок схема поиска минимума по алгоритмам, реализующим метод Фибоначчи и метод золотого сечения

Тогда экстремальная задача (3.3) выбора наилучшего метода F* при выполнении условий (3.10), (3.12) и (3.45) сводится к следующей задаче оптимизации:

min (1 — t*)^N. (3.46)

при условии, что

0 ≤ t* < 1/2; (3.47)

t²* — 3t* + 1 = 0. (3.48)

Из равенства (3.48) получаем, что t*= (3 ±√5)/2.

Но в силу ограничения (3.47) оптимальным решением экстремальной задачи (3.46)—(3.48) является параметр:

t* = (3 — √5)/2 = 0,381966010.

Комментарии запрещены.