Множество D называется допустимой областью изменения управляемых параметров х. Любой вектор х, принадлежащий допустимой области D (х∈D), определяет работоспособный (в смысле удовлетворения техническим требованиям, заданным системой неравенств (1.7)—(1.8)), вариант проектируемого устройства. По своей структуре допустимая область D может оказаться выпуклым или невыпуклым множеством, которое, в свою очередь, может быть односвязной или многосвязной областью.

Множество точек, образующих область D, называется выпуклым, если для любой пары точек х¹, х² ∈ D отрезок прямой линия, соединяющий их (х = αх¹ + (1 — α) х², 0 ≤ α ≤ 1), также полностью принадлежит этому множеству. (На рис. 1.1 приведены примеры выпуклого и невыпуклого множеств управляемых параметров х₁ и х₂.)

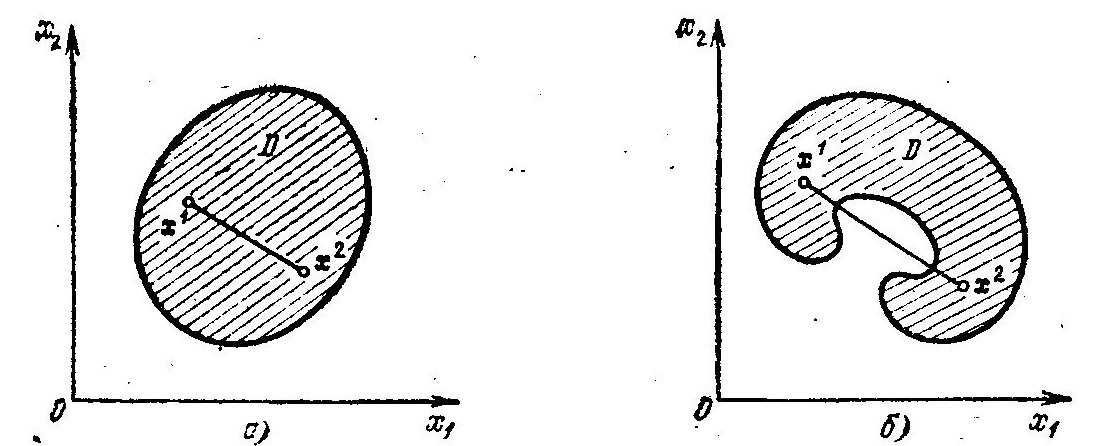
Рис. 1.1. Выпуклое (а) и невыпуклое (б) множество D управляемых параметров x₁ и x₂

Допустимая область D называется многосвязной, если она состоит из нескольких отдельных частей (выпуклых или невыпуклых), которые не Связаны между собой. В противном случае допустимая область D называется односвязной. На рис. 1.2 приведены примеры односвязной области D.

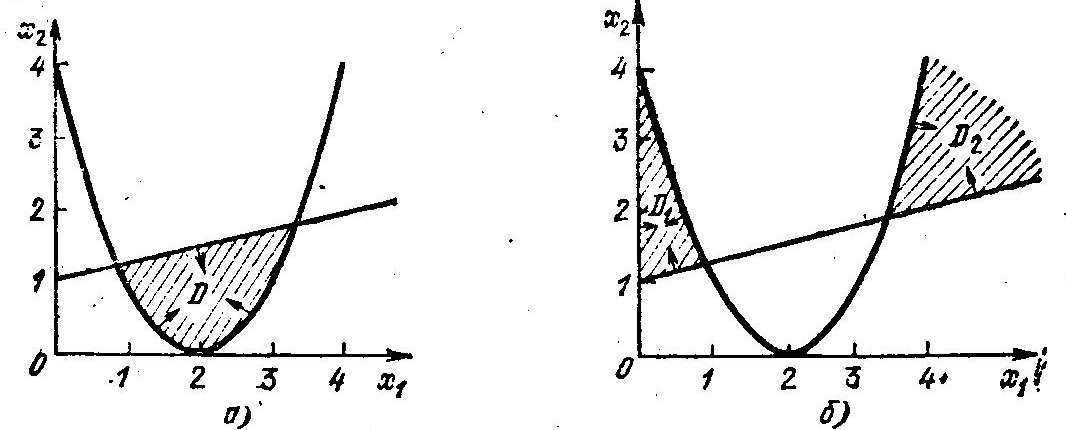
Рис. 1.2. Односвязная D (а) и многосвязная D₁ и D₂ (б) допустимая область управляемых параметров x₁ и х₂

D = {x|g₁ (х) = 0,25х₁ — х₂ + 1 ≥ 0, g₂ (х) = х₂ — х₁² + 4x₁ — 4 ≥ 0, х₁ ≥ 0, х₂ ≥ 0}

и многосвязной области D*, состоящей из двух частей D₁ и D₂:

D* = D₁∪D₂ = {х|g₁(х) = — 0,25x₁ + х₂ — 1 ≥ 0, g₂(х) = — x₂ + х₁² — 4x₁ + 4 ≥ 0, х₁ ≥ 0, х₂ ≥ 0}.

Одной из особенностей задач оптимального проектирования электронных схем является то, что в систему ограничений (1.9) могут входить характеристики, которые непрерывно зависят от некоторого параметра v, заданного на интервале [v^—, v⁺]. Таким параметром может быть частота, время, температура и т. п. Например, при проектировании транзисторных усилителей, пассивных и активных фильтров технические требования к частотным характеристикам (коэффициенту передачи по напряжению, входному и выходному импедансу, рабочему затуханию и т. д.) связаны с выполнением условий, чтобы в полосе пропускания Е_п частотная характеристика φ(х, ω) лежала в заданных пределах (φ_0^—, φ_0⁺), а в полосе задерживания Е_з была не меньше заданного значения φ_1^— (рис. 1.3):

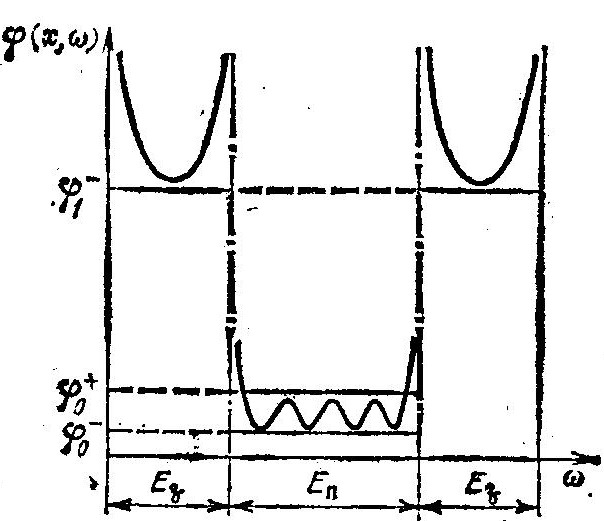
Рис. 1.3. Спецификация, отражающая требования к частной характеристике φ (х, ω) в полосе задерживания Е_з и полосе пропускания Е_п

φ_0^— ≤ φ(х, ω) ≤ φ_0⁺, для всех ω∈Е_п (1.16)

φ_0^— ≤ φ(х, ω), для всех ω∈Е_з. (1.17)

Аналогичные ограничения возникают при постановке задачи оптимального проектирования электронных схем с учетом старения элементов, т. е. с учетом постепенного и непрерывного изменения параметров компонент схемы со временем:

x_j = f_j(x_j⁰, t), j= 1, 2,…, n, (1.18)

где x_j⁰ — значение j-го параметра компоненты схемы в начальный момент времени.

Зависимости (1.18) могут быть как линейными, так и нелинейными функциями от времени t. Однако в силу нелинейной зависимости характеристик φ_i (х) от управляемых параметров х, выражения

φ_i(х) = φ_i (f₁(x₁⁰ t), f₂ (x₂⁰, t), …, f_n (x_n⁰, t) = φ_i * (х^o, t)

по параметру t будут иметь немонотонный характер. Для обеспечения работоспособности проектируемого устройства в течение времени гарантийной наработки Т характеристики φ_i * (х^o, t) должны находиться в пределах норм технических требований (φ_i^—, φ_i⁺):

φ_i^—≤ φ_i* (x^o, t)≤φ_i⁺, для всех t ∈[t₀, Т].

Таким образом, при решении задач оптимального проектирования электронных схем приходится рассматривать ограничения, которые связаны с выполнением условия

g(x, v)≥0, для всех v∈[v^—, v⁺] (1.19)

Переход от ограничений типа (1.19) к ограничениям (1.9), не зависящим от параметра у, можно осуществить либо при помощи сеточного метода, либо используя принцип гарантированного результата.

Комментарии запрещены.