Алгоритм, реализующий метод внутренних точек, можно представить в виде следующей последовательности действий.

1. Из решения вспомогательной задачи находится начальное приближение х°, принадлежащее множеству внутренних точек D₀, и принимается х_r⁰ = х°. (Если априори точка x°∈D₀ известна, то этот этап опускается.)

2. По формуле определяется начальное значение параметра штрафа c_k = c₀. (В общем случае значение c₀ > 0 может быть выбрано произвольным образом.)

3. Одним из методов, рассмотренных ранее решается задача безусловной минимизации для фиксированного значения параметра штрафа с_r из начальной точки х_r°:

min Ф(х, c_r) = min {(Q(x) + c_r∑(1/g_i)}.

Оптимальное решение этой задачи х_r* принимается за начальную точку следующей итерации: x_r+1⁰ = х_r*.

4. Проверяется условие окончания поиска оптимального решения
x* исходной задачи нелинейного программирования:

R(x_r*, c_r) = |c_r∑(1/g_i)| < δ.

Если это условие выполняется, то процесс поиска оптимального решения x* закончен и точка x_r* принимается за приближенное решение исходной задачи. В противном случае переходим к п. 5.

5. Изменяется значение параметра штрафа c_r таким образом, чтобы с ростом номера итерации r его значение уменьшалось, стремясь к нулю (например, можно считать, что c_r+1 = c_r/β, где β > 1). Весь процесс поиска повторяется с п. 3.

Недостатком рассмотренного алгоритма является то, что он требует существования «внутреннего множества» D₀ допустимой области D, т. е. он не позволяет решать задачи нелинейного программирования с ограничениями типа равенств. Кроме того, для использования этого алгоритма необходимо знать начальное приближение х°, в котором все ограничения удовлетворяются как строгие неравенства.

В связи с этим рассмотрим штрафную функцию Ф(х, c_r), для которой не требуется знать х°∈D₀ и которая позволяет решать задачи нелинейного программирования с ограничениями типа равенств так же легко, как и с ограничениями типа неравенств.

Предположим, что второе неравенство в условиях Куна—Таккера выполняется в ослабленном виде:

g_i(x) > -c_r, i = 1, 2, …, m.

Введем множители Лагранжа следующим образом:

u_i = — min [0, g_i (х)].

Тогда в точке минимума х* из последнего равенства условий Куна— Таккера можем записать

∇Q(x) + ∑min[0, g_i(x)]∇g_i(x)/c_r = 0.

Полученное выражение означает, что точка х_r* является локальным минимумом штрафной функции Ф(х, с_r) с квадратичным штрафом R (x, c_r)

Ф(x, c_r) = Q (x) + 1/c_rψ(x). (7.92)

Если точка x° находится вне допустимой области D, то движение осуществляется из недопустимой области в допустимую таким образом, чтобы минимизировать значение штрафа за выход точки х из области D. В допустимой области Ф (х, с_r) = Q (х), а вне области D значение R (х, c_r) очень велико по сравнению с Q (х).

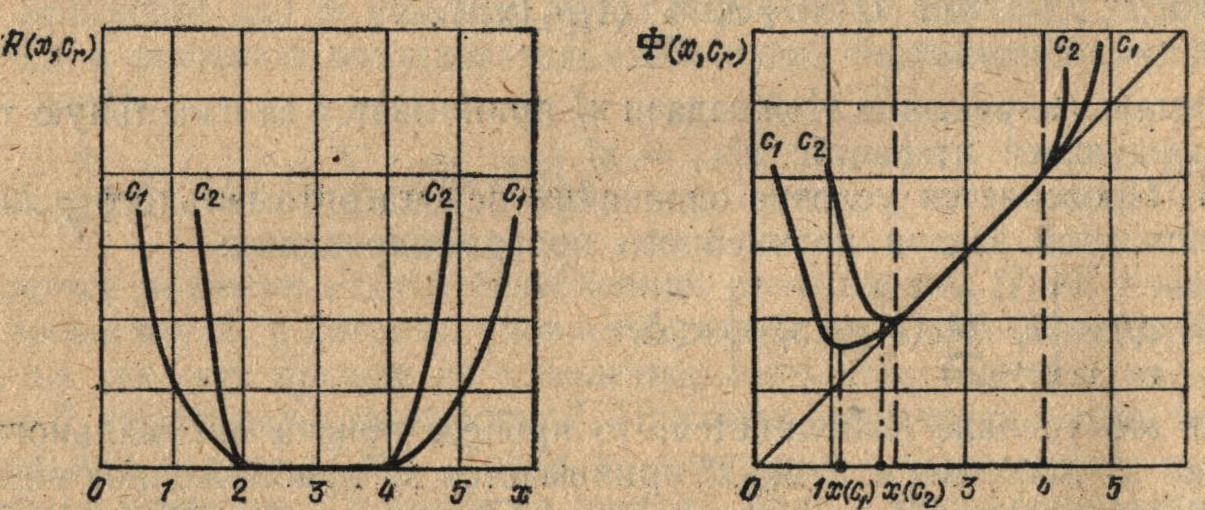
Рис. 7.6. Линии уровня штрафа R(x, c_r) (а) и штрафной функции Ф(х, c_r) (б) при c₁ > c₂ > 0 для задачи одномерной оптимизации min {x}

На рис. 7.6 в качестве иллюстрации приведены линии уровня штрафа R(х, с_r) = 1/с_r{(min [0, (х — 2)])² + (min [0, (4 — x)])²} и штрафной функции Ф (х, c_r) при различных значениях параметра c_r(c₁ > c₂ > 0) для задачи одномерного поиска min {х}.

Комментарии запрещены.