Образовательный блог — всё для учебы

Задача 2

Издержки одной типичной фирмы, работающей на конкурентном рынке, зависят от объема выпуска q как ТС = 5Q2 + 2Q. Рыночная цена на продукцию фирмы 12 руб.
Определите, будет ли фирма получать экономическую прибыль или нести убытки; какой уровень рыночной цены позволит фирме получать нормальную прибыль в долгосрочном периоде.
Прочитать остальную часть записи »

Система обслуживания с относительным приоритетом. Дадим теперь пример системы массового обслуживания, описание которой хотя и укладывается в схему (1.5), но не укладывается в схему кусочно-линейных преобразований, определенных в примере 5.

Пусть в однолинейную систему поступает N рекуррентных потоков требований, т. е. в k-м потоке требования поступают через случайные промежутки времени, являющиеся независимыми одинаково распределенными случайными величинами с функцией распределения Н_k(х), 0 ≤ х < ∞. Прочитать остальную часть записи »

Геометрические свойства знакоопределенной функции Ляпунова V(x)

1. Если функция V(x) знакоопределенная, то поверхность V(x₁, …, x_n)=c=const в пространстве (x₁, …, x_n) является замкнутой поверхностью (рис.3.1).
Прочитать остальную часть записи »

Обобщая полученный результат (1.52) на многомерный случай, для задачи (1.29) безусловной минимизации многопараметричеекой унимодальной функции Q (х) можем сформулировать следующие условия оптимальности.

Для того чтобы точка х*∈Rⁿ являлась оптимальным решением (локальным минимумом) необходимо и достаточно, чтобы в этой точке градиент минимизируемой функции равнялся нулю, а ее гессиан был положительно определенной матрицей:
∇Q(x*) = grad Q(x*) = 0 или

∂Q/∂x_j, j = 1,2,…, n; (1.55)
x^TG(x*)x > 0 для любых х ≠ 0. (1.56)

Прочитать остальную часть записи »

Отражатель используется для снижения утечки нейтронов из АЗ. Располагается вокруг АЗ. Отражатель повышает вероятность избежать утечку нейтронов ω и способствует выравниванию энерговыделения в АЗ. Если не менять свойства размножающей среды, то для поддержания критического состояния V_аз↓. Вводится понятие эффективной добавки (эффекта) отражателя δ.
R — R₀ = δ.
Прочитать остальную часть записи »

Лемма 1. Если S₁ — ς(ϑ)-оператор, S₁ : ϑ→ψ, S₂ς(ψ)-оператор, S₂:ψ→β, то оператор S = S₂S₁ является ς(ϑ)-оператором.
Прочитать остальную часть записи »

Какие же это процессы? В SQL – сервере – 3 или 4, Interbase – 1, Oracle до 16 фоновых процессов – 16 программ, одновременно сидящих в памяти и занятых собой. Среди них есть обязательные и есть работающие периодически.

Обязательные:
• Dbwr – Процесс записи в БД. Отвечает за перезапись данных из системной области SGA в файлы базы данных, после чего буфер очищается, т.е. из буфера ОП пишет на диск.
Прочитать остальную часть записи »

Будем говорить, что задача параметрической оптимизации (1.24), представляющая собой обобщенную математическую модель принятия решения в задачах оптимального проектирования, является разрешимой, если критерий оптимальности Q (х) достигает своего минимального значения в некоторой внутренней или граничной точке х* допустимой области D. Как отмечалось выше, вектор х* называется оптимальным решением. Естественно возникает вопрос: «Какие условия должны выполняться в точке х∈D, чтобы она являлась оптимальным решением?» В общем случае, не имея информации о классе функций, образующих критерий оптимальности и ограничения, такие условия, называемые условиями оптимальности (необходимыми и достаточными условиями минимума), сформулировать трудно. Поэтому рассмотрим часто встречающиеся на практике классы моделей принятия решений, которые являются частным случаем задачи параметрической оптимизации (1.24).
Прочитать остальную часть записи »

Определение 1. Функции из множества ς = ς(ϑ) назовем ς(ϑ) -функциями (или, короче, ς-функциями). При этом функции из набора ϑ будем называть образующими.

Рассмотрим набор {l₁, …, l_m} линейных функций:
Прочитать остальную часть записи »

Теорема (о СДНФ):

Всякая тождественно не равная 0 функция f(x₁, x₂,…,x_n) допускает представление f(x₁, x₂,…,x_n) = ∀_f(C1,…,C_n)x^C1₁…x^Cn_n (1) , где дизъюнкция берется по всем наборам C=(C₁,…,C_n) из 0 и 1, для которых f(c) = 1
Прочитать остальную часть записи »

Приближенную модель апериодического звена в форме разностного уравнения можно получить из соответствующего дифференциального уравнения

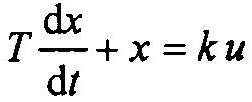
Заменяем дифференциалы приращениями на интервале квантования по времени
Прочитать остальную часть записи »

В свою очередь обобщением задачи квадратичного программирования является задача геометрического программирования, в которой критерий оптимальности и ограничения представлены с помощью положительных полиномов (позиномов):

g_i(x) = ∑ c_ijx₁^α_ij1x₂^α_ij2…x_n^α_ijn (1.39)

Прочитать остальную часть записи »

Пример 3.
Многолинейная система обслуживания с ожиданием. Система обслуживания состоит из N параллельно работающих приборов, на которые в моменты t_n поступают требования θ_n = t_n+1 — t_n. Пусть η_n — время обслуживания n-го требования. Если все приборы заняты, то требования образуют очередь и в дальнейшем обслуживаются в порядке поступления. Если поступившее требование застало в системе свободным хотя бы один прибор, то оно сразу направляется на обслуживание (безразлично, на какой прибор).
Прочитать остальную часть записи »

Топка (топочное устройство) – техническое устройство, предназначенное для преобразования химической энергии предварительно подготовленного топлива в тепловую, для частичной передачи этой тепловой энергии рабочему телу и для отвода продуктов сгорания от топочного объема.
Прочитать остальную часть записи »

Задачи 1. Найти точки экстремума (критические точки) для функций:
1) V₅(x₁, x₂) = x₁ — 3 x₂ + x₁ x₂,
2) V₆(x₁, x₂) = x₁³ — x₂² — 2x₁²,
3) V₇(x₁, x₂) = 3x₁² + x₂² — x₁³,
4) V₈(x₁, x₂) = x₁³ +4 x₂³+ x₂⁴.
Прочитать остальную часть записи »

Если в допустимой области D изменения управляемых параметров имеется только одно значение вектора х, то проблемы принятия решения не возникает. В тех же случаях, когда работоспособный вариант проектируемого устройства не единственен, для сравнения нескольких вариантов и выбора среди них наилучшего (в некотором смысле) необходимо ввести критерий оптимальности (функцию цели, критерий эффективности) Q (х), экстремальное значение (максимум или минимум) которого численным образом характеризует свойство одного из наиболее важных технико-экономических показателей проектируемого устройства.
Прочитать остальную часть записи »

Пример 1.
Цепь Маркова со счетным числом состояний. Пусть Z = {0, 1, 2, …}. Тогда процесс z_t называется однородной цепью Маркова со счетным числом состояний. Здесь этот процесс не связывается с описанием какой-либо конкретной системы, поскольку он применяется в самых разнообразных ситуациях. Как известно, динамика однородного марковского процесса полностью определяется матрицей переходных вероятностей Р=(Р_ij), i, j = 0, 1, 2, … В соответствии с формулой (1.1) действие производящего оператора А задается выражением

AV(k)= ∑p_kj V(j)-V(k). (1)

Прочитать остальную часть записи »

Семинар 1.

Задача 6

Производственная функция задана формулой Q = 5К•L. Цена единицы труда составляет 150 д.е., цена единицы капитала – 1000 д.е. Какова оптимальная комбинация ресурсов для производства товаров в количестве 1000 единиц? Как изменятся минимальные издержки производства того же количества товаров, если цена единицы труда повысится до 200 д.е.? Решить эту задачу геометрически и алгебраически.
Прочитать остальную часть записи »

Файлы инициализации

В большинстве СУБД, особенно крупных, таких как Informix, Sybase, Oracle, обязательным элементом архитектуры СУБД являются специальные файлы инициализации. Простые текстовые файлы, которые можно редактировать в блокноте, либо в DOS’е. Во многих из них указывается перечень настраиваемых параметров и их значения – oracle – init.ora. В том числе размер системный глобальной области (SGA – System Global Area), места расположения различных файлов, включая файлов транзакций и разных других журналов.
Прочитать остальную часть записи »

Сеточный метод основывается на замене интервала [v^—, v⁺], на котором определена характеристика g (х, v), ε-сетью v_ε, состоящей из s равномерно расположенных точек v_i. Прочитать остальную часть записи »

Рассмотрим процессы, у которых временной параметр t принимает значения в множестве Т = {0, 1, 2, …}. Такие процессы (с дискретным временем) представляют собой наиболее простую модель функционирования реальных систем. Вместе с тем они широко используются, так как позволяют зачастую элементарными средствами получать содержательные сведения о поведении системы.
Прочитать остальную часть записи »

Множество D называется допустимой областью изменения управляемых параметров х. Любой вектор х, принадлежащий допустимой области D (х∈D), определяет работоспособный (в смысле удовлетворения техническим требованиям, заданным системой неравенств (1.7)—(1.8)), вариант проектируемого устройства. По своей структуре допустимая область D может оказаться выпуклым или невыпуклым множеством, которое, в свою очередь, может быть односвязной или многосвязной областью.
Прочитать остальную часть записи »

Мы рассмотрели основные математические модели непрерывных систем. Но при решении задач с применением ЭВМ (будь-то задача управления или задача моделирования) исследователь сталкивается с дискретными процессами, связанными как с квантованием по уровню, так и с квантованием по времени.
Прочитать остальную часть записи »

А. Свойство регулярности
Хорошо известно, что существуют дифференциальные уравнения, решения которых определены лишь до некоторого конечного момента. Поэтому, если данные уравнения являются моделью какой-либо системы, то различные ее свойства могут изучаться лишь на конечном интервале времени. В то же время, как правило, требуется, чтобы движение системы было задано на бесконечном интервале времени. В связи с этим появилось свойство неограниченной продолжаемости решений, название которого говорит само за себя. Свойство иметь конечное время определения известно и для случайных процессов, когда может происходить накопление точек скачков процесса в конечные моменты времени либо, как и для решений дифференциальных уравнений, совершаться «уход в бесконечность» за конечное время. Ясно, что такие явления не присущи реальным системам, поскольку такие нерегулярности связаны в этом случае с бесконечной скоростью расходования некоторых ресурсов. Моделирование на ЭВМ процессов, обладающих указанными нерегулярностями, принципиально невозможно, так как любая из них влечет аварийную остановку процесса счета. Поэтому при создании математической модели некоторой системы необходимо проверить, удовлетворяет ли она свойству регулярности.
Прочитать остальную часть записи »

Любая характеристика φ_i(х) проектируемого устройства, математическое описание которого задано соотношениями (1.5), полностью определяется вектором управляемых параметров х. В процессе проектирования стремятся выбрать численные значения составляющих этого вектора х_i, i = 1,2,…, n, таким образом, чтобы удовлетворить техническим требованиям, предъявляемым к проектируемой схеме. Эти требования весьма разнообразны и определяются многими условиями, среди которых можно отметить следующие:
Прочитать остальную часть записи »

Развитие вычислительной техники и средств передачи информации привело к появлению сложных технических систем управления, что, в свою очередь, потребовало создания методов анализа и синтеза таких систем. Существующие методы количественного анализа оказываются, как правило, неэффективными при их применении к системам, описываемым сложными стохастическими процессами. Это объясняется несколькими причинами.
Прочитать остальную часть записи »

Свойства, характеризующие влияние внешних условий на функционирование, проектируемого устройства, описываются внешними параметрами. Этими параметрами могут быть начальные состояния физической системы s(t₀), входные воздействия z (t), конкретные значения времени t_i или частоты ω_k, температура окружающей среды и т. д. Внешние параметры можно разделить на параметры, имеющие постоянные значения, и на параметры, которые являются случайными величинами. Случайные внешние параметры будем называть внешними факторами и обозначать вектором ξ = (ξ₁, ξ₂,…, ξ_l).
Прочитать остальную часть записи »

В последнее время весьма интенсивно развивались исследования сложных многокомпонентных систем в самых разнообразных областях науки: экономике, биологии, социологии, градостроительстве, технологии и т. д.

Эти исследования стимулировались не столько абстрактной жаждой познания мира, сколько вполне конкретными причинами, связанными с необходимостью целенаправленно управлять такими системами, прогнозировать их развитие, устранять нежелательные явления в функционировании систем, повышать их общую эффективность. Конечно, не следует забывать и те возможности, которые предоставляет для таких исследований современный уровень научно-технического прогресса. Сейчас он выступает не толь¬ко как инструмент, как средство, но и как мощный стимул, побуждающий заниматься исследованием и решением проблем крупного масштаба.
Прочитать остальную часть записи »

Влияние изменения нагрузки на потери:

a. Реальные котлы работают в широком диапазоне нагрузок, при этом тепловые потери изменяются по-разному:

b. q₂ = (ϑ_ух, ϑ_ух), D↓ → ϑ_ух ↓, α_ух ↑. Т.к. q₂ больше зависит от ϑ_ух, то q₂ ↓.
c. q₂ возрастает при D ↓. Это вызвано понижением температуры в топке ϑ_m, а на котлах с ТШУ еще и тем, что отключаются отдельные горелки, при нагрузке менее 70%.
d. q₅↑ при D ↓. q₅ = q₅^ном×D^ном/D
Прочитать остальную часть записи »

Процедуру построения функционально-структурной модели проектируемого устройства можно охарактеризовать следующей последовательностью действий:

— выбирается его принципиальная электрическая схема;

— элементы схемы представляются в виде двухполюсных и многополюсных компонент;
Прочитать остальную часть записи »