Проблемно-ориентированные модульные системы программирования позволяют быстро формировать из компонентов модель исследуемой системы. Однако формирование модели является лишь начальным этапом исследования. Для его реализации необходимо обеспечить целый комплекс дополнительных средств.

В первую очередь речь идет о воспроизведении на ЭВМ среды функционирования исследуемой системы.

Среда функционирования включает разнообразные сигналы, действующие на реальную систему. Сигналы и воздействия можно разделить на две группы:
• детерминированные,
• случайные, стохастические.

В общем случае детерминированными называются такие сигналы и процессы, знание которых в данный момент позволяет определить их значения в любой последующий момент.

Имеется большое разнообразие детерминированных сигналов и воздействий. Представим типовые детерминированные воздействия, используемые при исследовании динамических систем (рис. 1).
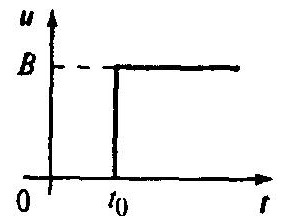
1. Ступенчатое воздействие или единичный скачок:
u(t-t₀) = B, t>t₀;
u(t-t₀) = 0, t0.

Этот сигнал характеризует сброс и наброс нагрузки, включение и выключение питания или другого воздействия. Такой сигнал позволяет оценить динамические характеристики непрерывных систем и объектов — с её помощью оценивается переходная функция.

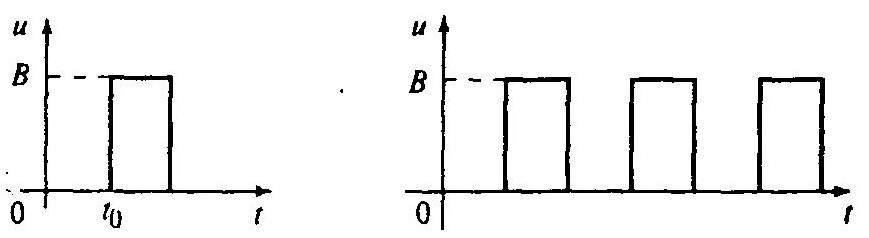
2. Одиночный импульс и периодическая последовательность импульсов. Такие сигналы воспроизводят кратковременные и повторяющиеся удары.

3. Гармонический сигнал:

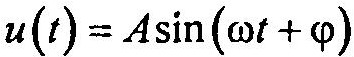
Широко используется при исследованиях динамических систем в частотной области.

а) единичный скачок, ступенчатое воздействие

б) одиночный импульс и последовательность импульсов

в) гармоничный сигнал

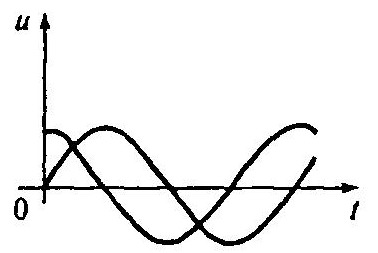
Г) Дельта импульс

4. Дельта-импульс — некоторая идеальная математическая модель:

5. Площадь такой функции равна единице; дельта-функция применяется для получения весовых функций.

Реализация детерминированных сигналов на ЭВМ не представляет каких-либо трудностей.

Более сложную задачу представляют воспроизведение случайных сигналов и воздействий, их имитация.

Комментарии запрещены.