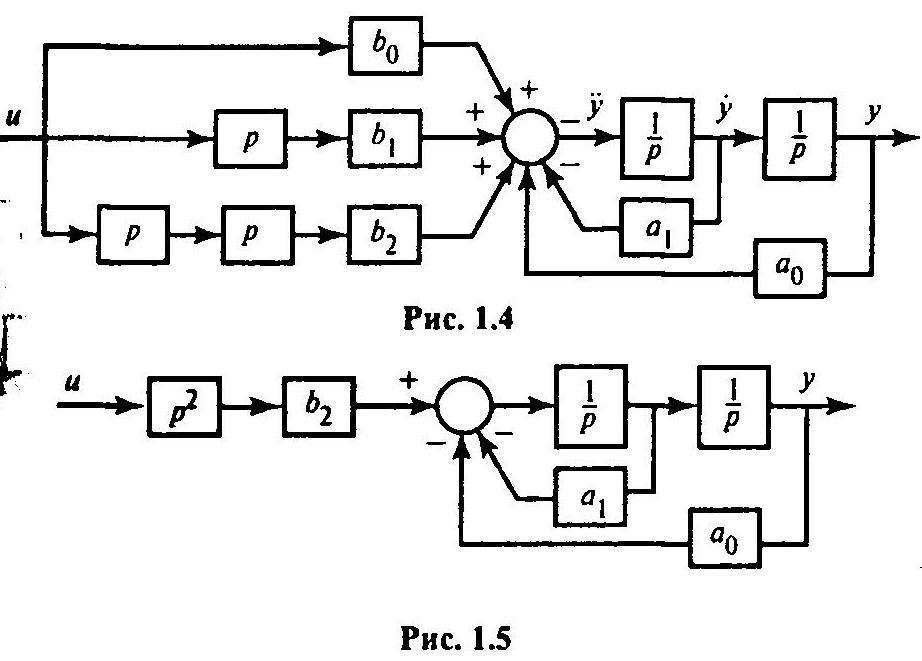
Модель в переменных состояния
Исходными уравнениями являются дифференциальные уравнения динамических систем. Рассматриваемый метод представляет собой метод понижения порядка дифференциального уравнения посредством последовательного интегрирования.
В результате получаются схемы, в основе которых число интеграторов равно порядку дифференциального уравнения.
Пусть динамическая система описывается дифференциальным уравнением вида
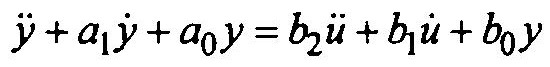
Запишем уравнение относительно высшей производной у:
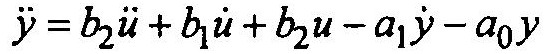
Основу схемы составят два интегратора (рис. 1.5).