Инструментальное средство автоматизации моделирования непрерывных динамических систем
Многие реальные системы являются нелинейными и подвержены воздействию стохастических сигналов и помех.
Здесь представляется одна из последних версий известного программного комплекса МАСС (машинный анализ и синтез систем), предназначенного для моделирования, анализа и параметрического синтеза непрерывных в общем случае нелинейных динамических систем и процессов, заданных структурными схемами и дифференциальными уравнениями.
По организации программного обеспечения МАСС представляет собой развитый пакет прикладных программ. Пакет МАСС построен по принципу отдельных загрузочных модулей, работающих под управлением главной программы.
Основные функции, выполняемые в программном комплексе МАСЛИН, реализуются и в пакете прикладных программ МАСС.
Важнейшую компоненту пакета МАСС представляет язык моделирования, с помощью которого пользователь в состоянии описать систему, среду функционирования и цели ее исследования. Основу языка составляет набор функциональных блоков. Каждый блок выполняет определенную функцию, которой соответствует программный модуль. Библиотека языка моделирования включает более 70 типов функциональных блоков.
Эта библиотека позволяет моделировать:
• дифференциальные уравнения и передаточные функции типовых и нетиповых динамических звеньев;
• наиболее распространенные нелинейные характеристики;
• элементарные математические функции;
• арифметические операции;
• среду функционирования, т.е. внешние воздействия;
• специальные блоки — для реализации произвольных однозначных нелинейностей, для расширения функций системы (блоки пользователя, макроблок).
Кроме того, возможности проблемно-ориентированного языка расширены за счет включения в библиотеку блоков, реализующих дискретные элементы и логические функции. Блочно-ориентированный язык обеспечивает непроцедурное программирование. Непроцедурное программирование выражается еще и в том, что порядок ввода блоков в ЭВМ при составлении машинной модели произвольный, т.е. пользователь освобождается от каких-либо требований по порядку ввода компонентов модели. Пакет прикладных программ МАСС необходимое упорядочение блоков для построения вычислительной схемы осуществляет автоматически.
С блоками, используемыми в пакете МАСС, с технологией ввода структуры и параметров модели, можно познакомиться в соответствующей литературе. Пакет прикладных программ МАСС ориентирован на персональный компьютер. Минимальный объем памяти на магнитном носителе — 320 Кбайт. Взаимодействие пользователя с пакетом программ МАСС осуществляется в интерактивном графическом режиме.
В состав пакета входят модули:
• графический редактор структурных схем;
• модуль преобразования структурных схем из графического в цифровое представление;
• модуль численного интегрирования и визуализации рассчитанных зависимостей;
• модуль параметрической оптимизации;
• модули для подключения блоков пользователя»
• файлы «помощь» (HELP).
Функциональный состав пакета МАСС представлен на рисунке ниже. Функцию любого блока из библиотеки функциональных блоков можно представить в виде Y = F (Х,Р), где X — входы блока, Р — параметры блока.
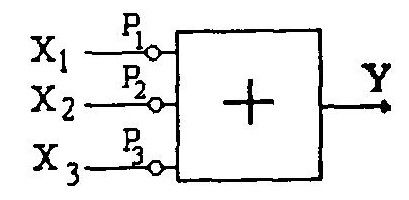
Максимальное число входов и параметров блока — 3, число выходов — 1. Так, весовой сумматор с идентификатором «+» имеет три входа — x1, x2, x3 и три параметра — Р1, Р2, Р3 (значения весов).
Y = P1X1 + P2X2+P3X3.
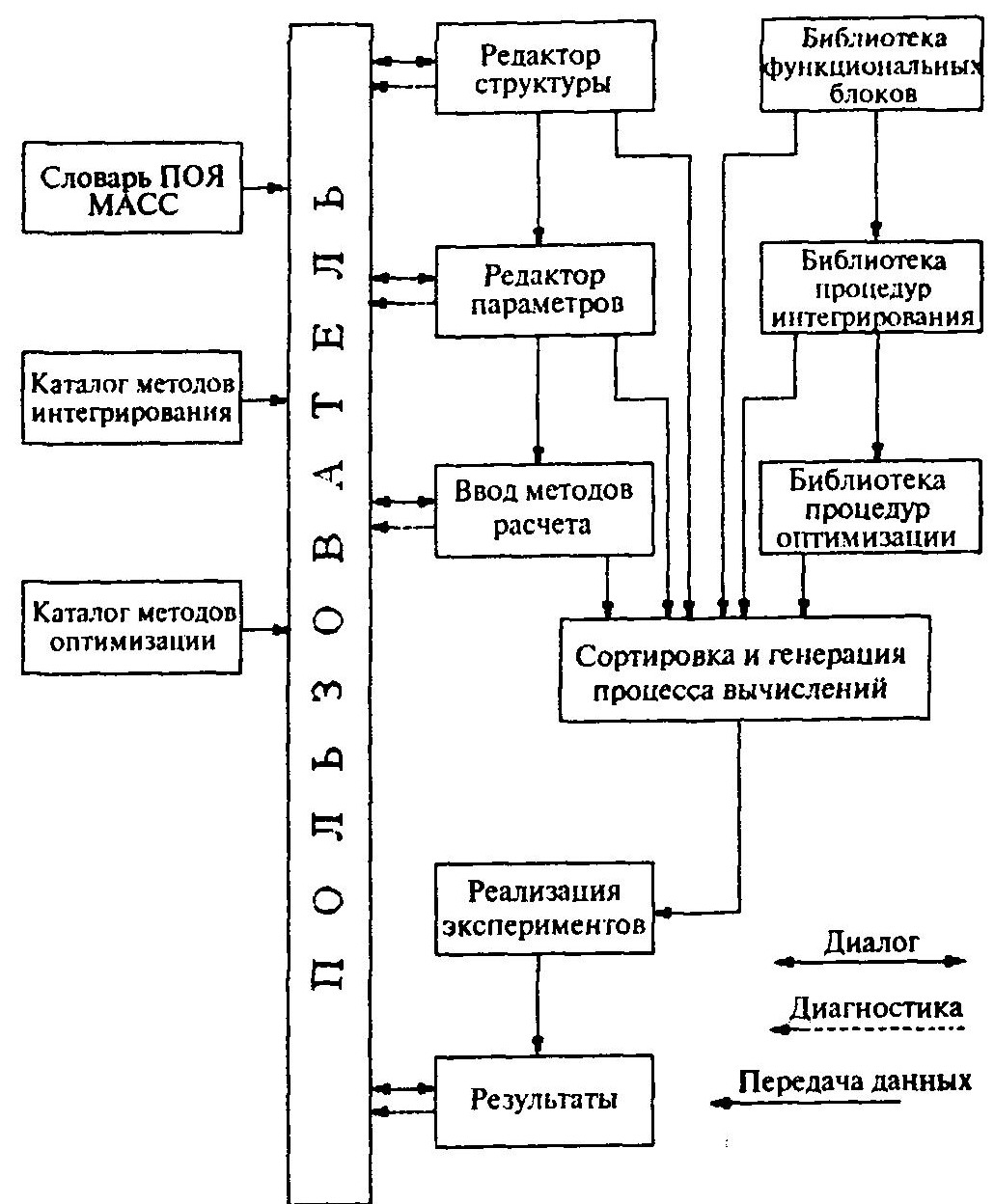
Функциональный состав пакета МАСС
Интегратор с идентификатором IN имеет три входа, два параметра P2 и P3, а P1 задает начальное условие:
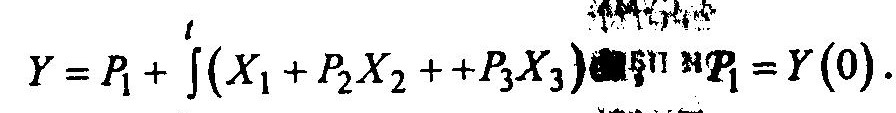
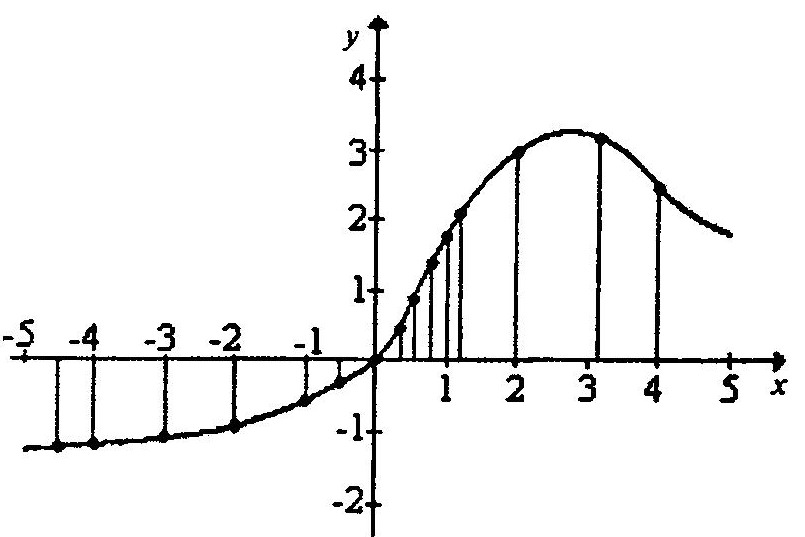
Графически заданная произвольная, нестандартная нелинейная функция
Есть ряд функциональных блоков для расширения возможностей системы. Например, блок FG (Function Generation) позволяет генерировать нетиповые нелинейные функции. Не все нелинейности можно представить типовыми моделями нелинейных характеристик и не все нелинейные характеристики могут быть описаны аналитически.
Пусть имеем графически заданную произвольную, нестандартную нелинейную функцию (рисунок выше).
В заданных пределах функция Y может быть представлена значениями ординат в 50 точках. Эти точки по оси абсцисс должны следовать друг за другом в порядке возрастания.
Может встретиться необходимость в реализации специальных алгоритмов, которых нет в библиотеке модулей пакета МАСС или для реализации которых потребуется большое количество блоков библиотеки. Тогда можно воспользоваться блоками пользователя. В этом случае пользователь пишет алгоритм блока на языке ПАСКАЛЬ в виде подпрограммы-функции. Вид соответствующего файла и требования к оформлению подпрограммы имеется в соответствующей литературе. После включения этого блока пользователя в пакет МАСС к нему можно обращаться как к основным типовым блокам.
Имеется еще целый ряд вспомогательных блоков для реализации логических функций и моделирования импульсных и цифровых систем.
Секции численного интегрирования и оптимизации представлены, как и в системе МАСЛИН, набором соответствующих методов.
При решении оптимизационных задач ПОЯ позволяет воспроизвести практически любой необходимый критерий. С помощью ППП МАСС процессы в исследуемой системе могут быть представлены как во временной области, так и фазовом пространстве.
Рассмотрим основные алгоритмы функционирования пакета МАСС. Для пользователя ввод модели в ЭВМ осуществляется очень просто. Ввод модулей для формирования модели осуществляется в любом порядке. Но ЭВМ не может решать задачу, осуществлять необходимые вычисления для произвольной последовательности модулей. Задача получения правильной вычислительной схемы решается автоматически с помощью алгоритма планировщика (или сортировки), которая и определяет последовательность обработки модели. Рассмотрим алгоритм работы планировщика. В процессе ввода модели в ЭВМ каждый модуль занимает строку в матрице структуры (таблице) в той последовательности, в какой их вводит пользователь. После окончания ввода модели в ЭВМ начинает работать алгоритм планировщика. Задача планировщика установить очередность обработки функциональных модулей — вычисление может выполняться, если известны значения входов модуля.
Таблица — Матрица структуры
| № строки | Тип блока, идентификатор | Предвключенный блок на 1-й вход | Предвключенный блок на 2-й вход | Предвключенный блок на 3-й вход |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| … | … | … | … | … |
| n-1 | ||||
| n |
Последовательность обработки модулей заносится в специальный массив ORDER, называемый вектором порядка расчета. Можно выделить две фазы работы планировщика:
1-я фаза — в упорядоченный список сразу включаются модули, не имеющие входов (например, константа К, системное время T);
2-я фаза — просматривается матрица структуры, начиная с первой строки.
Если предвключенные блоки для блока в первой строке находятся в упорядоченном списке (ORDER), то блок в первой строке тоже заносится в упорядоченный список, если нет, то осуществляется просмотр последующих строк и так далее до строки, блок которой можно занести в упорядоченный список. В этом случае алгоритм возвращается к первой строке и снова начинает просмотр строк матрицы структуры — возможно изменялась ситуация и какой-то блок можно занести в массив ORDER. Этот цикл продолжается до тех пор, пока все блоки не окажутся в упорядоченном списке. Но может встретиться ситуация, когда не все блоки попали в упорядоченный список. В этом случае выдается диагностическое сообщение — обнаружен так называемый алгебраический контур и вычисления не могут быть выполнены.
Алгебраический контур включает блоки типа К, T и другие и не содержит ни одного динамического звена. Такие контуры характеризуют вырожденные ситуации.
Допустим, обнаружен алгебраический контур. Представим полный граф такого контура. Возьмем один из блоков этого контура — его можно считать основанием дерева. Будем считать каждый последующий блок как бы основанием нового дерева и т.п. При полном обходе контура окажется, что невозможно построить дерево, так как некоторый блок на его ветви окажется основанием предшествующего дерева, что соответствует замкнутой петле — своего рода цикл. Решение не имеет продолжения. Надо развязать такую петлю. Это можно сделать:
1) преобразованием схемы модели, чтобы петля исчезла;
2) ввести в контур дополнительное динамическое звено. Последнее поясним на примере (рисунок ниже).
Пусть фрагмент схемы модели, в которой отсутствуют блоки с памятью имеет вид
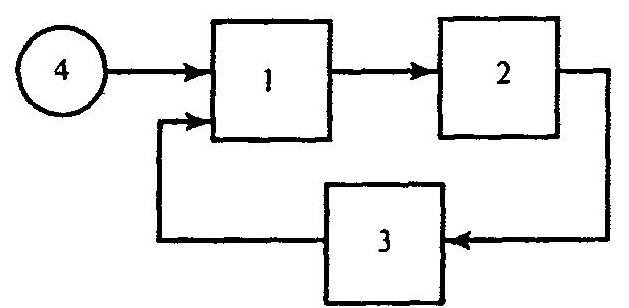
Фрагмент схемы модели, в которой отсутствуют блоки с памятью
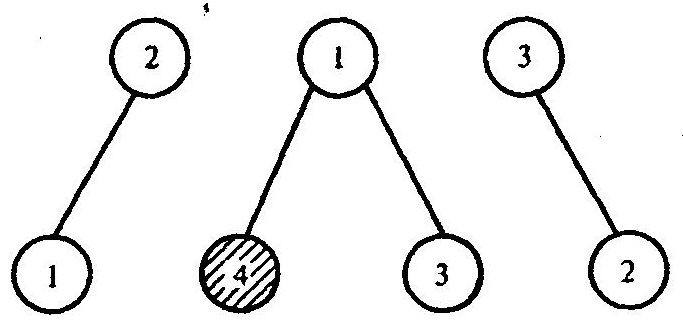
Строительство дерева с блока 2
Блок 4 считается известным и его можно сразу поместить в упорядоченный список. Блоки 1,2,3 не являются динамическими. Начнем строить дерево с блока 2 (рисунок выше). Заштрихован блок с известным входом. Здесь блок 2, находящийся на ветви третьего дерева, является основанием первого дерева, т.е. контур замкнулся и решения нет. Введем вместо блока 1 динамический блок — блок задержки на полтакта DU. Соответствующий граф контура с DU принимает вид, представленный на рисунке ниже.
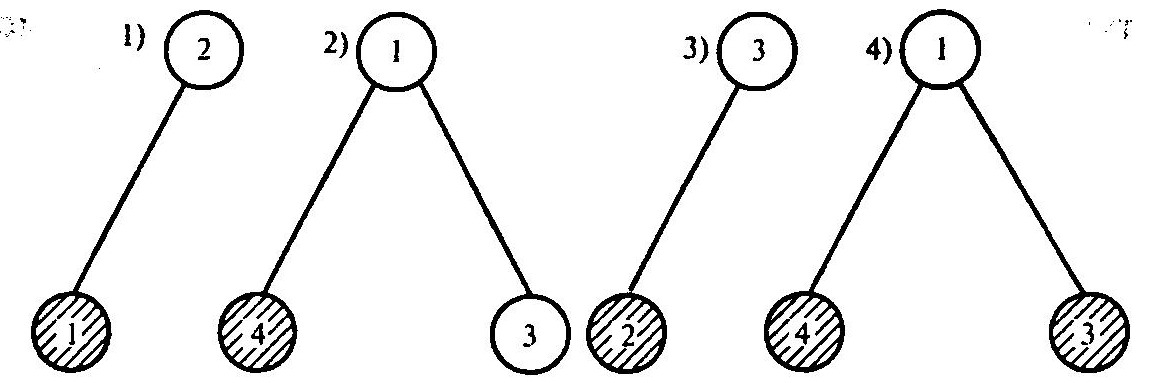
Граф контура с DU
В упорядоченный список сразу помещается блок 4, затем блоки 2 и 3 и, наконец, блок 1. Элемент DU с памятью сначала замещается известным значением выхода в начальный момент, а затем в процессе расчетов его состояние перевычисляется (начиная со второго такта).
Итак, исследуемая модель строится посредством соединения произвольно вводимых пользователем программных модулей.
Возникает задача получения правильной вычислительной схемы, т.е. правильной последовательности обработки модулей. При решении на ЭВМ уравнение n-го порядка надо преобразовать в систему из п дифференциальных уравнений первого порядка (форма Коши). ППП МАСС автоматически программирует такую систему, осуществляет машинную реализацию динамических звеньев.
Предварительно отметим следующее важное обстоятельство. При записи передаточной функции общего вида как отношения полиномов или в виде соответствующего дифференциального уравнения появляются производные от управляющего воздействия. Если управляющее воздействие не дифференцируемо m раз (m — степень числителя передаточной функции), то правая часть дифференциального уравнения терпит разрыв непрерывности. Чтобы избежать неприятностей, связанных с этим, надо преобразовать систему уравнений так, чтобы дифференциальные уравнения не содержали производных от входного сигнала.
А теперь, рассмотрим, как это делается. Сначала представим общую схему решения. При структурном представлении динамических систем имеем дело с передаточными функциями вида
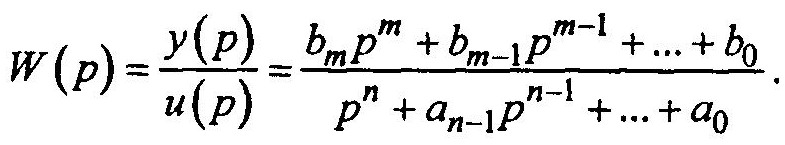
Соответствующая ей система дифференциальных уравнений первого порядка в форме Коши может быть получена на основе следующей эквивалентной схемы (если использовать способ построения схемы методом понижения порядка), представленной на рисунке ниже.
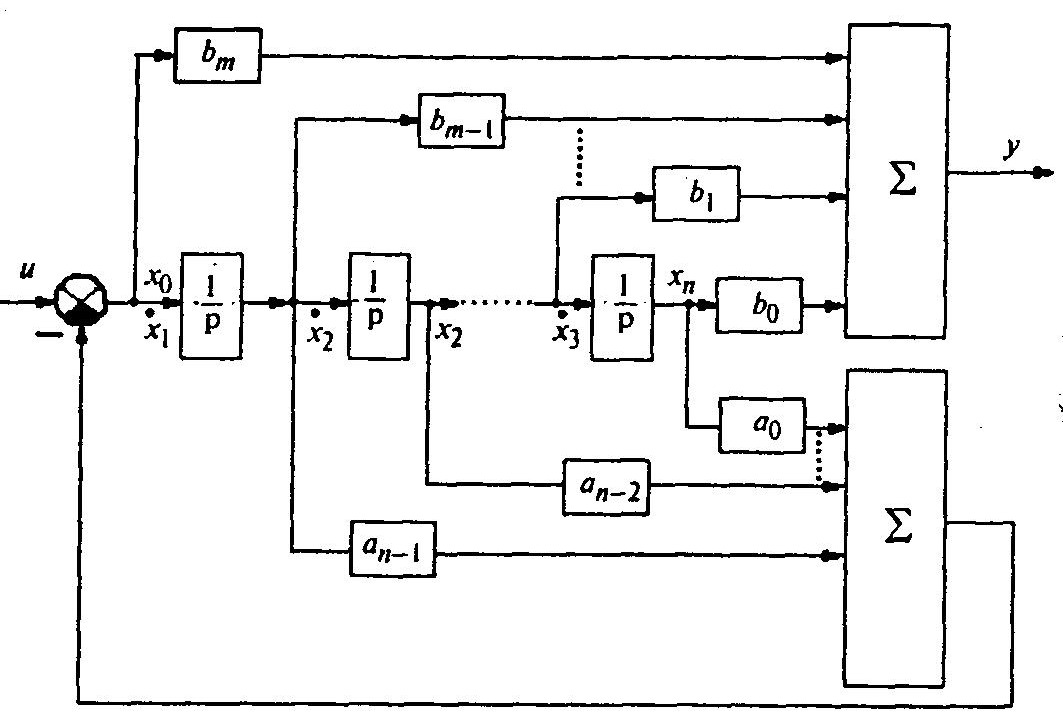
Способ построения схемы методом понижения порядка
Эту схему можно получить, если сделать простейшие преобразования с исходной передаточной функцией. Разделим числитель и знаменатель на рn и перепишем передаточную функцию в виде
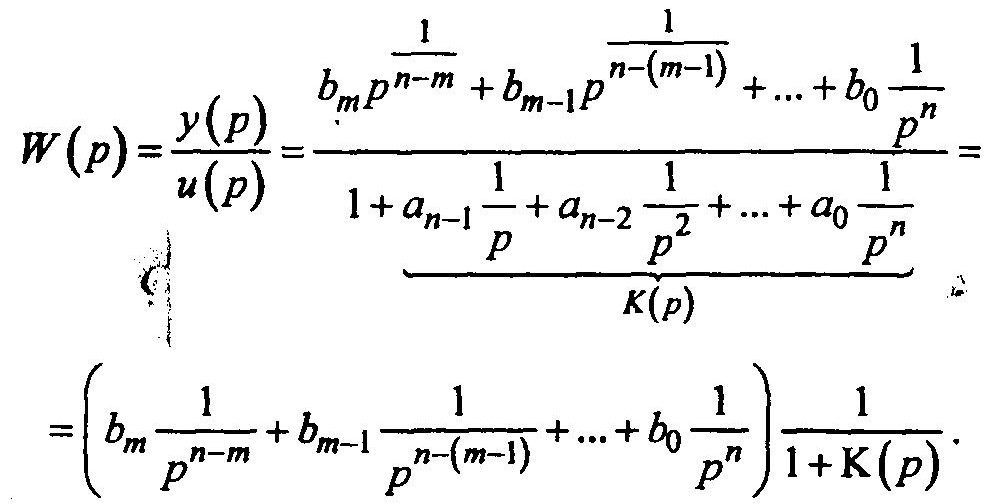
Первый сомножитель (см. верхнюю часть схемы) представляет собой как бы воздействие на ошибку, места съема сигналов зависят от степени р при коэффициентах bj. Так, в общем случае, если m = n, при bm будем иметь р в нулевой степени.
Поэтому сигнал ошибки проходит только через коэффициент bm. При коэффициенте b(m-1) будем иметь 1/p и снимается сигнал после первого интегратора и т.д.
Второй сомножитель является передаточной функцией ошибки замкнутой системы, представленной на рисунке ниже.

Функция ошибки замкнутой системы
На основе общей схемы запишем систему дифференциальных уравнений в форме Коши. Здесь переменные состояния формируются на основе ошибки и ее производных (принимая х’1 = х0). В результате получаем
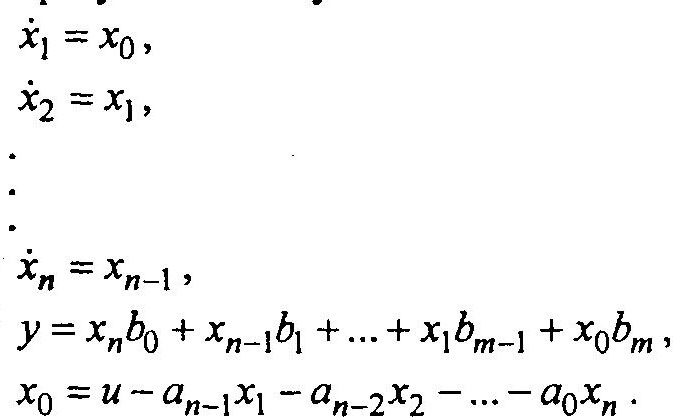
Динамические блоки ППП МАСС на ЭВМ программно реализуются на основе подобных схем замещения. Покажем это на примере реализации звена второго порядка.
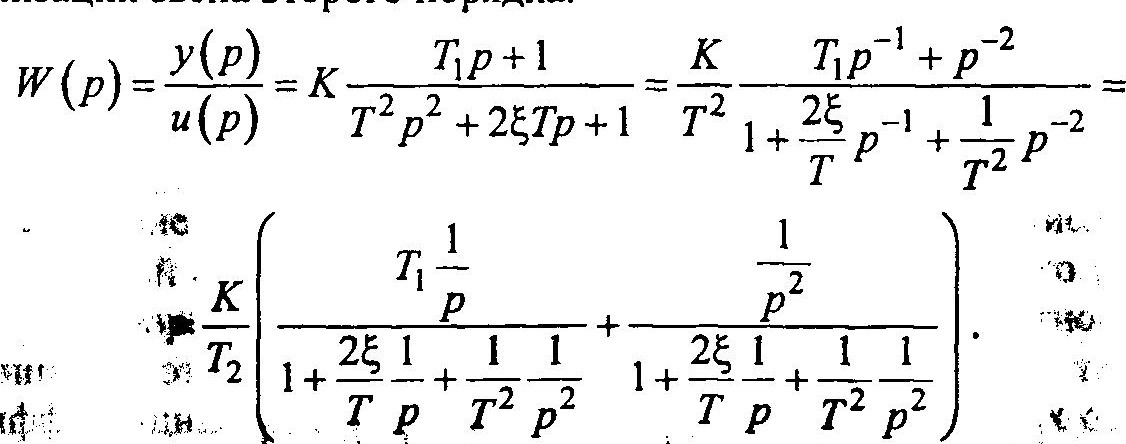
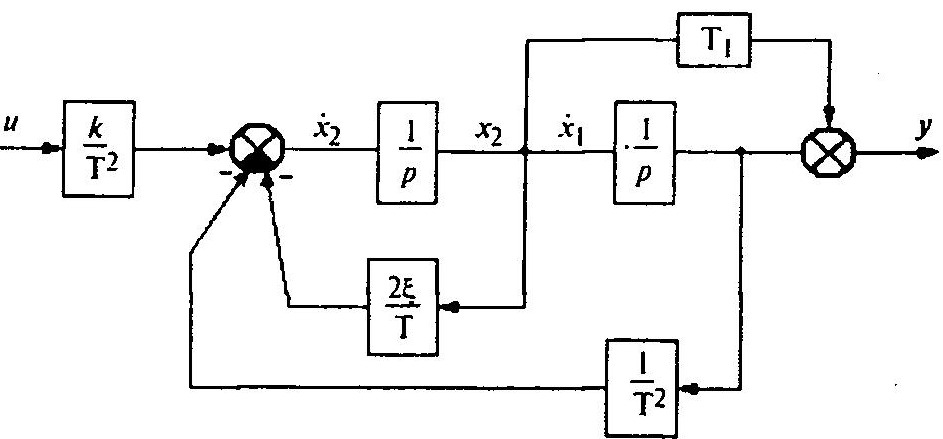
Схема звена второго порядка
Схема звена второго порядка приведена на рисунке выше. Соответствующие дифференциальные уравнения имеют вид:
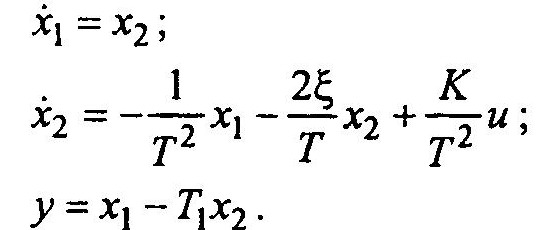
Итак, МАСС — пакет моделирования динамических систем, модели которых составляются из отдельных блоков. В МАСС реализованы принципы визуально-ориентированного непроцедурного программирования, основанного на выборе нужных блоков из библиотеки системы и соединения их для составления модели анализируемой системы или устройства. При этом уравнения состояния, описывающие работу моделей, формируются автоматически. МАСС представляет собой открытый пакет, что позволяет его легко пополнять и расширять.
Представим примеры, иллюстрирующие возможности МАСС.
Пример 1. Рассмотрим процесс во временной области в цепи RLC.
Уравнение этой цепи имеет вид
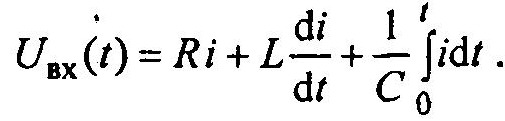
Т.к. i=C dU /dt, то уравнение можно записать в виде
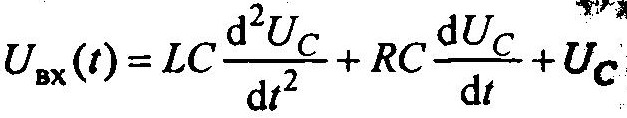
Перепишем это уравнение в эквивалентном виде относительно второй производной выходного сигнала
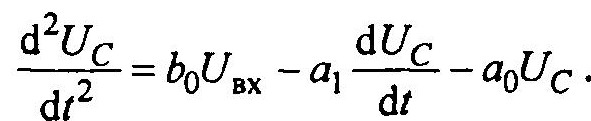
Используем метод понижения порядка дифференциального уравнения. Для получения решения относительно Uc = Uвых надо дважды проинтегрировать последнее уравнение.
В результате получим модель цепи, представленную на
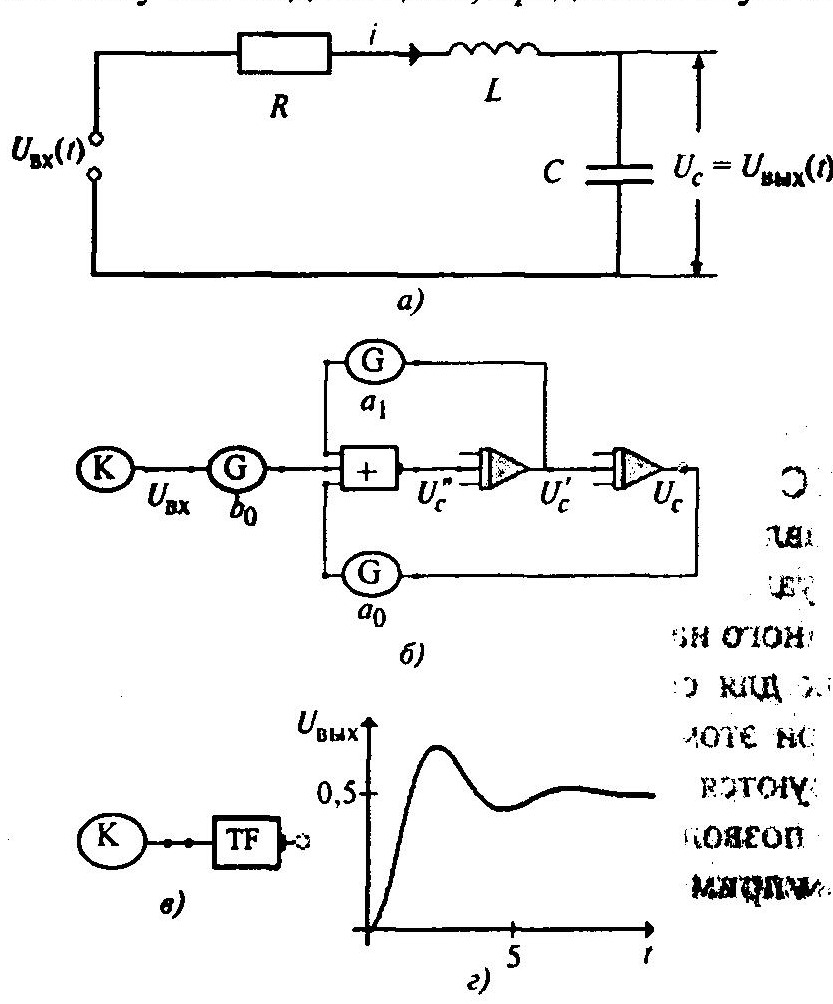
Другую модель рассматриваемой цепи можно представить, если перейти к описанию цепи с помощью передаточной функции. Для этого применим преобразование Лапласа к уравнению (7.2):
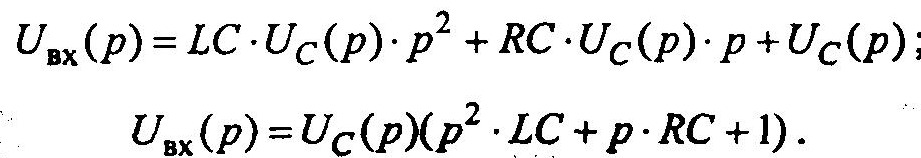
Тогда передаточная функция, связывающая вход и выход цепи, имеет вид:
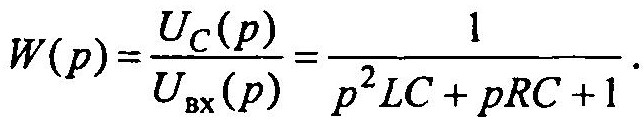
Используя блок TF пакета МАСС, представим другую модель RLC-цепи с теми же значениями параметров R, L и С, что и в предыдущей модели. Блок К воспроизводит скачкообразное входное воздействие. Выходной сигнал данной модели совпадает с выходным сигналом предыдущей модели.
Пример 2. Представим фазовый портрет нелинейной системы, модель которой на ПОЯ МАСС приведена на рисунке ниже. Эта модель отображает нелинейную систему с гистерезисом Н, инерционным звеном AN, интегратором I и сумматором «+».
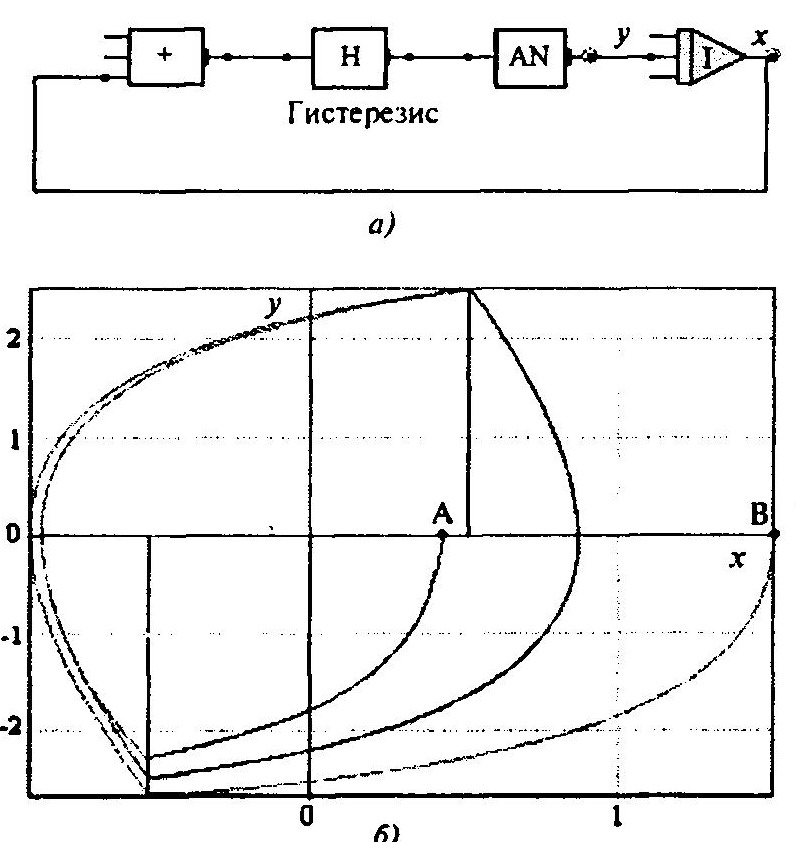
Рассматривается поведение автономной системы (нет внешних воздействий) при различных начальных состояниях, которые задаются начальными условиями на интеграторе.
Если обозначим выход интегратора (системы) через х, а выход инерционного звена через y, то y=dx/dt (x и y – оси координат фазовой плоскости). Фазовый портрет рассматриваемой системы представлен на рисунке выше. Из портрета видно, что в такой автономной системе возникают автоколебания, соответствующие устойчивому предельному циклу, к которому сходятся фазовые траектории из различных начальных условий (точки А и Б).
Пример 3. Если исследуемая модель сложная и содержит много компонентов (функциональных блоков), то её можно упростить посредством представления частей модели в виде отдельных макроблоков. Макроблок (MB) может содержать блоки In (входы) для связей с другими частями моделируемой системы. Для вывода сигнала из MB надо отметить выход нужного блока в MB. Отметим, что пользователь может изменить параметры элементов, входящих в MB.
Для вычисления среднеквадратического отклонения на рисунке ниже представлен MB. Нелинейный блок D позволяет избежать деления на нуль.
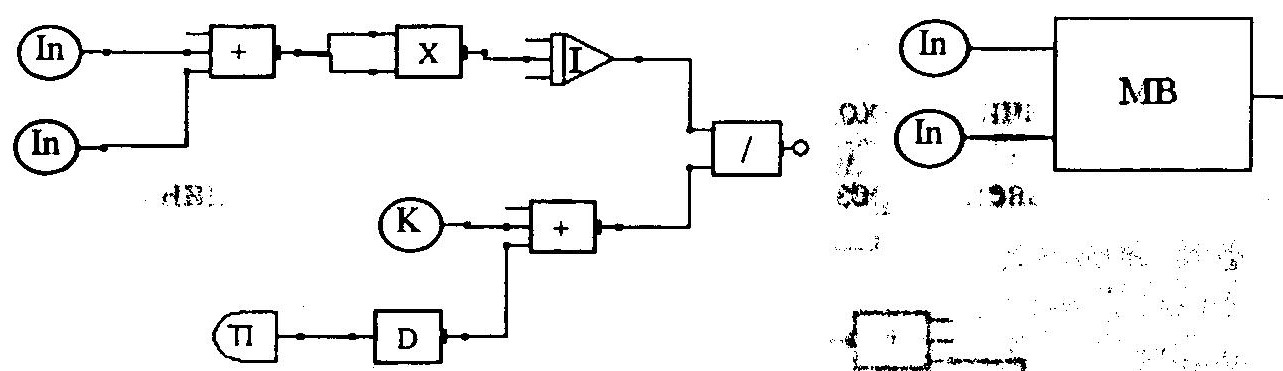
Полученным MB можно оперировать так же, как любым другим функциональным блоком ПОЯ МАСС.
Рассмотренные примеры раскрывают лишь малую часть возможностей ППП МАСС. С другими возможностями можно познакомиться в руководстве по применению МАСС и при решении учебных и исследовательских задач.