Численные методы интегрирования
Составление модели исследуемой системы соединением готовь программных модулей и воспроизведение сигналов, действующих на систему, является подготовительным шагом для имитационного исследования. Машинный эксперимент проводится в целях получения информации о характеристиках функционирования рассматриваемого объекта. Основная задача планирования машинных экспериментов — получение необходимой информации об исследуемой системе при ограничениях на ресурсы (затраты машинного времени, памяти и т.п.).
Важными являются проблемы обеспечения точности и достоверности результатов моделирования при заданном числе реализаций (объеме выборки) или оценка необходимого числа реализаций при заданных точности и достоверности результатов моделирования. Существуют методы решения указанных проблем.
Проблемы возникают при обработке и анализе результатов статистического моделирования, связанные с хранением большого объема промежуточных результатов. Эту проблему можно решить, используя рекуррентные алгоритмы обработки, когда оценки вычисляют по ходу моделирования.
Другими словами, для получения тех или иных оценок по результатам машинного эксперимента, важное значение имеют экономные в вычислительном плане методы обработки данных.
При имитационном моделировании динамических систем исследователь имеет дело с решением алгебраических и дифференциальных уравнений на ЭВМ. Речь идет о численном решении уравнений.
Как известно, для решения дифференциальных уравнений их представляют в форме Коши, т.е. в виде системы п дифференциальных уравнений первого порядка с заданными начальными условиями. Искомая функция (решение) y(t) ищется в отдельных точках сетки интервала [t0,tk], т.е. в конечном числе точек t0,t1,t2,…, tk, называемых узлами сетки.
В каждом узле определяются значения y0,y1,y2,…,yk, приближенно равные значениям точного решения ут (t0), yт (t1), yт(tk).
Расстояние между узлами h = Δt = tk+l — tk — шаг интегрирования. Шаг интегрирования может быть как постоянным, так и переменным.
Методы численного интегрирования различаются по степени использования информации с предыдущих шагов, по способу вычисления решения и т.п. В частности, по степени использования информации с предыдущих этапов решения численные методы бывают одношаговые и многошаговые, по способу вычислений — явные и неявные, по формуле прямоугольников, по формуле трапеций существует большое многообразие методов численного интегрирования. Поэтому в системах имитационного моделирования должен быть набор численных методов интегрирования, охватывающих широкий круг задач данной предметной области.
Выбрать наиболее подходящий метод для эффективного решения конкретной задачи не так просто.
Практика применения численных методов интегрирования показала целесообразность включения в этот набор различных модификаций метода Эйлера, методов Рунге—Кутта, методов прогноза и коррекции (Милна и Адамса-Мултона), методов решения жестких систем дифференциальных уравнений.
Система обыкновенных дифференциальных уравнений в форме Коши в общем случае имеет вид:
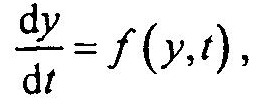
у(t0) = y0 — начальные условия;
f={f1,f2,…,fn}— заданная вектор-функция;
y={y1,y2,…,yn} —вектор искомых переменных.
В одношаговом явном методе Эйлера вычисление очередного Значения уk+1 осуществляется по формуле
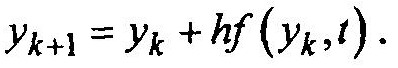
Здесь вычисление значения уk+1 производится с использованием только одного предыдущего значения уk.
Такие одношаговые методы называют еще самостартующими.
Методы Рунге—Кутта представляют собой класс одношаговых методов. Формулы Рунге—Кутта используют значения производной, определенной в нескольких точках внутри интервала вычислений. Для практических расчетов широко используется формула Рунге—Кутта четвертого порядка
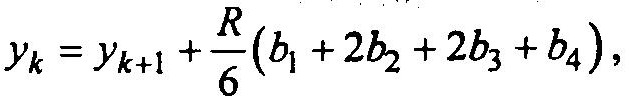
Где
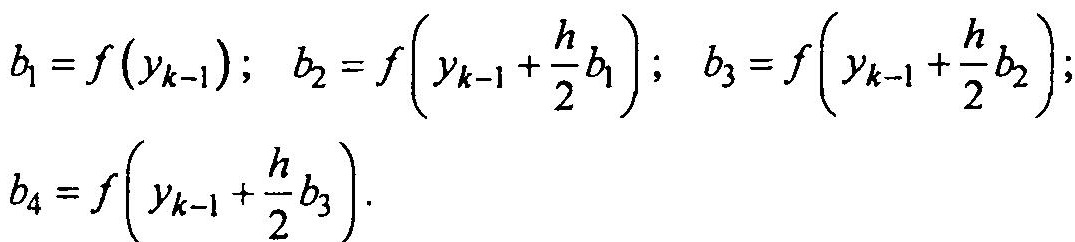
Достоинства метода Эйлера — простота и скорость расчета. Метод Рунге—Кутта обеспечивает более высокую точность и большое значение допустимого шага h.
При решении одних и тех же уравнений метод Эйлера дает менее точное решение, а Рунге—Кутта требует большое время расчета. Широко используется метод Рунге—Кутта четвертого порядка с переменным шагом.
Распространение получили методы на основе прогноза и коррекции Милна и Адамса—Мултона. В этих методах интегрирования производные, используемые для прогноза и коррекции, вычисляются два раза на каждом шаге по сравнению с четырьмя, в методе Рунге-Кутта. Поэтому для систем высокого порядка методы прогноза и коррекции дают значительную экономию времени, объема вычислений. Но методы прогноза и коррекции сложны для программирования и не являются «самоначинающимися».