График функции распределения F(x) в общем случае представляет собой график неубывающей функции, значения которой начинаются от 0 и доходят до 1, причем в отдельных точках функция может иметь скачки (разрывы).

Зная ряд распределения прерывной случайной величины можно легко построить функцию распределения этой величины.

Действительно: F(x) = P(X < x) = ∑_{xiP(X = xi)}

Суммирование распространяется на все значения x_i меньше x.
При прохождении текущей переменной x через какое-нибудь из возможных значений прерывной величины Х, функция распределения меняется скачкообразно, причем величина скачка равна вероятности этого значения.

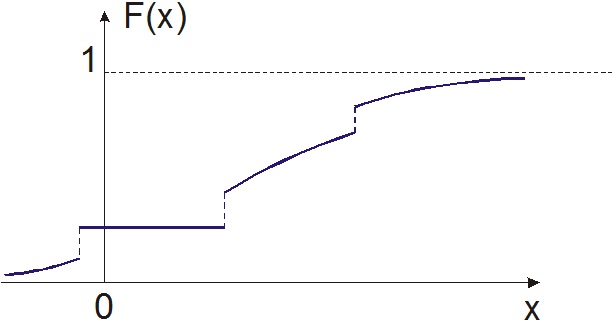
Функция распределения любой прерывной величины всегда есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины и равны вероятностям этих значений. Сумма всех скачков функции F(x)=1.

По мере увеличения числа возможных значений случайной величины и уменьшения интервала между ними, число скачков становится больше, а сами скачки меньше. Ступенчатая кривая становится более плавной. Случайная величина постепенно приближается к непрерывной, а ее функция распределения к непрерывной функции.

Вероятность попадания случайной величины на заданный участок
При решении практических задач, связанных со случайными величинами, часто оказывается необходимым вычислять вероятность того, что случайная величина X примет значение, заключенное в некоторых пределах от α до β: α ≤ X < β. Для определенности условимся левый конец α включать в участок (α, β), а правый нет: α ≤ Х < β. Выразим вероятность этого события через функцию распределения величины Х. Для этого рассмотрим три события: событие А, состоящее в том, что X < β; событие В, состоящее в том, что X < α; событие С, состоящее в том, что α ≤ Х < β. Событие А по теореме сложения вероятностей равно А = В + С и его вероятность Р(А) = Р(В) + Р(С) или P(X < β) = P(X < α) + P (α ≤ Х < β). Но вероятность нахождения случайной величины левее некоторой текущей переменной есть ни что иное, как функция распределения: F(β) = F(α) + P (α ≤ Х < β) откуда

P (α ≤ Х < β) = F(β) - F(α)

т.е. вероятность попадания случайной величины на заданный участок равна приращению функции распределении на этом участке. Будем неограниченно уменьшать участок (α, β), полагая, что β→α. В пределе вместо вероятности попадания на участок получим вероятность того, что величина примет отдельно взятое значение α:

P(X=α) = lim_β→α P(α ≤ Х < β) = lim_β→α [F(β) — F(α)]

Если в точке α функция F(x) имеет разрыв, то предел равен значению скачка функции F(x) в точке α. Если же функция F(x) в точке α непрерывна, то этот предел равен нулю. Тогда вероятность любого отдельного значения непрерывной случайной величины равна нулю.

Комментарии запрещены.