Повторение опытов

При практическом применении теории вероятностей часто приходится встречаться с задачами, в которых один и тот же опыт или аналогичные опыты повторяются неоднократно. В результате каждого опыта может появиться или не появиться некоторое событие А, причем нас интересует не результат каждого отдельного опыта, а общее число появлений события А в результате серии опытов. В подобных задачах требуется уметь определять вероятность любого заданного числа проявлений события в результате серии опытов. Они решаются весьма просто в случае, когда опыты являются независимыми.

Несколько опытов называются независимыми, если вероятность того или иного исхода каждого из опытов не зависит от того, какие исходы имели другие опыты.

Независимые опыты могут производиться в одинаковых или различных условиях. В первом случае вероятность события А во всех опытах одна и та же Р_i(А)=const. Во втором случае вероятность события А от опыта к опыту меняется Р_i(А)=var. К первому случаю относится частная теорема, а ко второму – общая теорема о повторении опытов.

Формулировка частной теоремы о повторении опытов:
Если производится n независимых опытов, в каждом из которых событие А проявляется с вероятностью р, то вероятность того, что событие А появится ровно m раз выражается формулой:

P_m,n = C_n^mp^mq^n-m (1)

где q = 1 — p, C_n^m — число всех комбинаций, т.е. число способов которыми можно из n опытов выбрать m в которых произошло событие А.

Формула общей теоремы:

∏ (q_i+p_iz) = ∑P_m,n z^m (2)

где z – произвольный параметр.

Как в общем, так и в частном случае:

∑P_m,n = 1 (3)

Случайные величины и законы их распределения
Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, неизвестно заранее какое именно.

Случайные величины бывают двух типов:
• непрерывные;
• прерывные (дискретные).

Условимся в дальнейшем случайные величины обозначать большими буквами, а их возможные значения – соответствующими малыми буквами.
Пример:
Х- число попаданий при трех выстрелах:
х₁ = 0;
х₂ = 1;
х₃ = 2;
х₄ = 3.

Рассмотрим прерывную случайную величину Х с возможными значениями x₁, x₂, …, x_n. Каждое из этих значений возможно, но не достоверно, и величина Х может принять каждое из них с некоторой вероятностью
Х= х₁;
Х= х₂;
Х= х₃;
Х= х₄.

Обозначим вероятности этих событий P(X=x₁) = p₁; P(X=x₂) = p₂; P(X=x_n)=p_n.

∑P_m,n = 1, так как несовместные события образуют полную группу. Эта суммарная вероятность каким-то образом распределена между отдельными значениями. Случайная величина будет полностью описана с вероятностной точки зрения, если будет задано это распределение, т.е. в точности указано, какой вероятностью обладает каждое из событий. Этим устанавливается так называемый закон распределения случайной величины.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Закон распределения прерывной случайной величины Х может быть задан в следующих формах:
• табличной;
• аналитической;
• графической.

Простейшей формой задания закона распределения прерывной случайной величины Х является таблица.

Такую таблицу называют рядом распределения случайной величины Х.

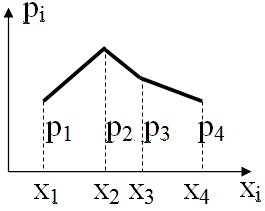
Чтобы придать ряду распределения более наглядный вид, часто прибегают к его графическому изображению.

Для непрерывной случайной величины такой характеристики построить нельзя!!!

Для непрерывной случайной величины удобно воспользоваться не вероятностью события Х=х, а вероятностью события Х<х, где х – некоторая текущая переменная. Вероятность этого события, очевидно, зависит от х и есть некоторая функция от х.

Комментарии запрещены.