Образовательный блог – всё для учебы

Определение: Степень вершины графа есть число инцидентных (принадлежащих) ей ребер. Граф G – четен, если каждая его вершина имеет четную степень.

Определение: Цикл (контур) в графе (орграфе) G называется Эйлеровым, если он проходит без повторов через все ребра (дуги) графа G. Граф (орграф) G называется Эйлеровым, если он имеет Эйлеров цикл (контур).

Замечание: Эйлеров граф связен ибо Эйлеров цикл связывает все вершины графа. Эйлеров цикл ориентирует ребра графа в направлении обхода цикла.

Теорема Эйлера: пусть G – связный граф, тогда граф G – Эйлеров ? G – четен.

Доказательство (необходимость) ?: пусть связный граф G – Эйлеров и C – есть его Эйлеров цикл. Каждое прохождение вершины при движении по циклу приносит 2 (добавляет 2 ребра) в степень этой вершины. Т.к. каждое ребро графа G появляется в цикле один раз, то все вершины в графе G имеют четные степени, т.е. граф G четен.

Достаточность?: пусть связный граф G – четен, тогда G имеет простой цикл С. Удалим из G ребра цикла C (сохранив в G их вершины.), снова получим четный граф, т.к. либо от вершины в G удалим два ребра цикла, если эта вершина принадлежит циклу С, либо число ребер в ней не меняется, если вершина не принадлежит С. Из получившегося четного графа, каждая компонента связности которого четна, можно снова выделить цикл и т.д. пока не придем к графу G, у которого нет ребер.

Таким образом граф G допускает представление в виде объединения простых циклов, попарно не пересекающихся по ребрам: G = C1?C2?…. ?Ck. Пусть С’ – есть один из этих простых циклов. Если G состоит только из простого цикла C’, то G – есть Эйлеров граф. Если G имеет другие простые циклы, то в силу связности графа G существует простой цикл C’’ имеющий общую вершину V с циклом C’ (при отсутствии в циклах C’ и C’’ общих ребер), тогда C’UC’’ – есть цикл с началом в вершине V, составленный сначала из ребер цикла C’, затем из ребер цикла C’’. Так циклу C’?C’’ последовательно принадлежат другие простые циклы, значит, получили цикл, проходящий через все ребра графа G, поэтому этот цикл является Эйлеровым ? граф G – также Эйлеров. Чтд.

Замечание: Теорема и ее Доказательство без изменения переносятся на мультиграфы и псевдографы. При этом петли относятся к одному из циклов, проходя их все при попадании в вершину, на которой эти петли навешаны. Т.к. петля прибавляет к степени вершины 2, то ? количество петель на четность вершины не влияет. Аналогичная Теорема справедлива и для орграфов.

Теорема: Связный орграф G – Эйлеров ? для каждой вершины v в G число входящих в V дуг (полустепень захода) равна числу исходящих из V дуг (полустепень исхода).
Без доказательства.

Замечание: (Алгоритм 2): Эйлеров цикл в четном графе можно построить начав его любым ребром, а затем последовательно надстроив его вправо смежным ребром, одновременно удалив выбранные ребра из графа и следя за тем, чтобы при очередном удалении ребра из графа он не распался на несвязные компоненты или не очутились в изолированной вершине, не исчерпав при этом всех ребер графа.

Полные циклы и последовательности де Брейна

Пусть E₂ⁿ – есть множество всех наборов (a₁…a_n) длины n из нулей и единиц.

Определение: Набор из нулей и единиц длины 2ⁿ – есть полный цикл (де Брейна), если множество последовательно прочитанных наборов длины n исчерпывает все множество наборов длины n из нулей и единиц.

Замечание: цикл де Брейна, как и все циклы, располагается по кругу, конец совпадает с началом.

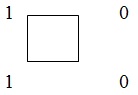
Полный цикл 0011- дает все наборы длины 2: 00,01,11,10

Теорема: для ?n существует полный цикл де Брейна.
Доказательство: Построим ориентированный псевдограф G следующим образом: вершины в G пометим набороми из 0 и 1 длины (n-1), тогда G имеет 2^n-1 набора вершин. Каждый набор a₁,…,a_n из E₂ⁿ длины n определяет дугу, соединяющую вершины (a₁,…,a_n-1) и (a₂,…,a_n). Граф G связен, ибо ? пара вершин (a₁,…,a_n-1) и (b₁,…,b_n-1) в G соединена следующим образом:
(a₁,…,a_n-1) ? (a₂,…,a_n-1, b₁) ? (a₃,…,a_n-1,b₁,b₂) ?….? (a_n-1, b₁,…,b_n-2) ? (b₁,…,b_n-1)

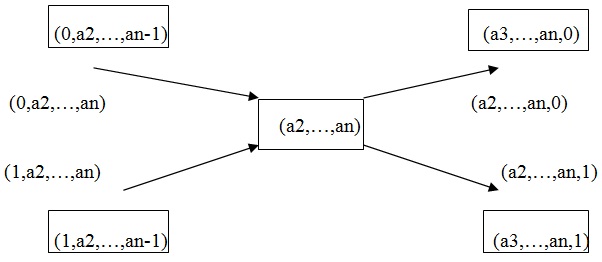
В каждую вершину (a₂,…,a_n) входят две дуги, помеченные наборами (0,a₂,…,a_n) и (1,a₂,…,a_n) и выходит 2 ребра, помеченные наборами (а₂,…,a_n,0), (a₂,…,a_n,1) ? степень каждой вершины в G четна. Полустепени захода и исхода для каждой вершины из G равны ? орграф G – Эйлеров ? он имеет Эйлеров контур, в котором каждая вершина проходится дважды, ибо ее степень равна 4, тогда первые компоненты наборов, которыми помечены вершины в этом обходе, дадут полный цикл де Брёйна.

Замечание: Теорема справедлива и для наборов (a₁, a₂,…,a_n) из E_kⁿ длины n с элементами из E_k = {0,1,…,k-1}

Гамильтоновы графы

Определение: Цикл С в графе G называется Гамильтоновым циклом, если С проходит без повторов вершин через все вершины графа G. Граф G – Гамильтонов, если G имеет Гамильтонов цикл.
Замечание: Определение Гамильтоновых и Эйлеровых графов схожи, но методы их исследования различны. Пока не найдены простые критерии (вместо переборного) гамильтоновости графа. Есть предположение, что их нет. Доказаны лишь некоторые достаточные условия гамильтоновости.

Теорема Поша: если связанный граф G:
1) имеет p ? 3 вершин.
2) для ?n из 1 ? n < (p-1)/2 следует условие, что число вершин со степенями ? n меньше n
3) из нечетности p следует, что число вершин степени (p-1)/2 меньше (p-1)/2 то G – есть гамильтонов граф.
Без доказательства.

Замечание: ограничивая условия теоремы Поста, получаем более простые, но менее сильные условия гамильтоновости графа.

Следствие 1(Оре): если число вершин графа G p?3 и сумма степеней вершин deg(u)+deg(v) ? p для ? пар несмежных вершин u и v в G, то граф G – гамильтонов.
Следствие 2 (Дирак): если число вершин графа G p?3 и deg(v)?p/2 для любой вершины v графа G, то G – Гамильтонов.

1. Формула Эйлера
2. Графы К5 и К33. Критерий планарности Понтрягина-Куратовского
3. Способы задания графов и операции над графами
4. Графы, мультиграфы, псевдографы, орграфы. Изоморфизм графов
5. Матричная теорема Кирхгофа о деревьях
6. Двудольные графы и парасочетания
7. Верхняя и нижняя оценки для хроматического числа. Внутренне и внешне устойчивые множества вершин графа
8. Перечисление графов. Производящая функция для числа помеченных графов с р вершинами
9. Линейное пространство подграфов данного графа
10. Деревья, их характеристика, каркасы (остовы)
11. Циклический ранг графа
12. Раскраска графов, хроматическое число и хроматический класс
13. Раскрашивание планарных графов. Теорема о пяти красках. Теорема о четырех красках
14. Оптимальная раскраска вершин графа
15. Двудольные и бихроматические графы
16. Планарные и плоские графы
17. Подпространство четных подграфов