Образовательный блог – всё для учебы

Пусть G=(V,E) есть (p,q) – граф с множеством V=(v₁, v₂,…, v_p) вершин и E=(e₁,e₂, …,e_q) – ребер. Пусть H⊆G – есть остовный подграф графа G с тем же множеством V вершин.

Подграфу H поставим в соответствие характеристический вектор.
a_Н ={a₁, a₂, …, a_n}, где i=1,2,…q и a_i равен:
- 1, если ребро e_i ∈ H
- 0, если ребро e_i ∉ H

Между множеством L_G^q всех основных подграфов графа G и множеством всех наборов из E₂^q можно установить взаимнооднозначное соответствие, при котором вектору a=(a₁, a₂, …, a_q) соответствует подграф H_a=(V, E_a) в котором ребро e_i ∈ E_a⇔ a_i=1. На множестве всех подграфов графа G определим сложение и умножение на const из E₂^q = {0,1} следующим образом. Пусть H, H₁, H₂ есть подграфы графа G и а_Н, а_Н1, a_Н2 есть соответствующие характеристические вектора. Пусть λ ∈ E₂, тогда:
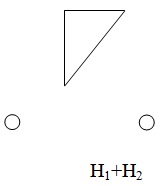
Подграф H₁+H₂ соответствует вектору a_Н1+a_Н2.
Подграф λ*H соответствует вектору λ*a_Н.
Подграф 0*H соответствует вектору 0*a_Н.

Потому содержит только вершины из G, но ни одного ребра. Подграф 1*H совпадает с H, ибо его характеристический вектор 1**a_Н = *a_Н.

Линейное пространство наборов E₂^q изоморфно системе подграфов L_G^q, потому система LGq есть линейное пространство. Размерность обоих пространств равна q, числу ребер в G.

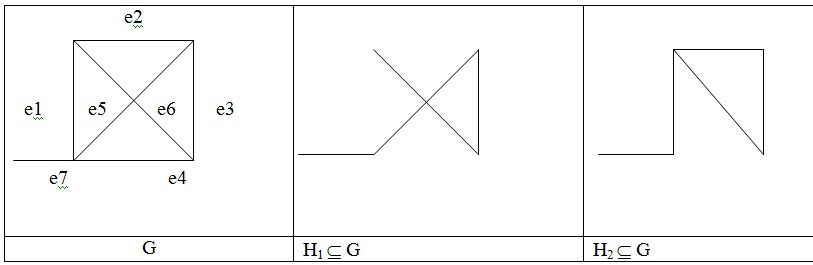
Им соответствуют вектора

a_H1+ a_H2 = (1,1,0,0,0,1,0) – ему соответствует подграф H₁+H₂

1. Подпространство четных подграфов
2. Циклический ранг графа
3. Оптимальная раскраска вершин графа
4. Графы, мультиграфы, псевдографы, орграфы. Изоморфизм графов
5. Фундаментальная система циклов
6. Обходы графа. Циклы Эйлера, Гамильтона, де Брейна
7. Верхняя и нижняя оценки для хроматического числа. Внутренне и внешне устойчивые множества вершин графа
8. Раскраска графов, хроматическое число и хроматический класс
9. Матричная теорема Кирхгофа о деревьях
10. Теорема Кэли о числе помеченных деревьев с р вершинами
11. Функции алгебры логики
12. Графы К5 и К33. Критерий планарности Понтрягина-Куратовского
13. Системы различных представителей, теорема Холла о совершенном паросочетании в двудольном графе
14. Класс монотонных функций и его замкнутость относительно суперпозиции
15. Двудольные графы и парасочетания
16. Способы задания графов и операции над графами
17. Раскрашивание планарных графов. Теорема о пяти красках. Теорема о четырех красках