Лавина электронов и условие самостоятельности разряда
Разряд в газе начинается с того, что свободные электроны, всегда в некотором количестве имеющиеся в газе, под действием приложенного напряжения приобретают энергию достаточную для ударной ионизации. Если при столкновении электрона с нейтральной молекулой происходит ионизация, то образуется еще один электрон, который так же может ионизовать, и процесс приобретает лавинный характер.
Действительно, пусть n — концентрация электронов. Тогда на пути dx в электрическом поле в результате ионизации образуется dn новых электронов

dn = nαdx (1)

Общее число электронов в лавине на пути dx получается интегрированием (1):

∫dn/n = ∫αdx или n=n₀e^αx, (2)

где n₀ — начальная концентрация электронов.

Выражение (2) справедливо в однородном электрическом поле. В неоднородном поле, в котором напряженность в промежутке меняется по пути движения лавины,
n = n₀exp∫αdx
При ионизации образуются не только электроны, но и положительные ионы, обладающие малой по сравнению с электронами подвижностью, поэтому по мере движения лавины к аноду в ней происходит процесс разделения зарядов. Электроны уходят на анод, а положительные ионы, подходя к катоду, создают там новые электроны за счет вторичной ионизации. Эти вторичные электроны также могут создавать лавины. Если интенсивность вторичной ионизации слабая и для поддержания воспроизводства электронов требуется действие внешнего ионизатора, то такой разряд называется несамостоятельным.

В случае, если процессы ионизации развиваются и при прекращении действия внешнего ионизатора, то образуется самостоятельный разряд.

Условие перехода разряда в самостоятельный процесс носит название условия самостоятельности разряда Таунсенда и может быть пояснено следующим образом.

Пусть в результате процессов ударной ионизации в промежутке между электродами формируется лавина электронов, которые под действием поля движутся к аноду. Соответственно положительные ионы движутся к катоду и выбивают вторичные электроны.

Для того, чтобы разряд поддерживался без действия внешнего ионизатора, нужно, чтобы процессы вторичной ионизации, сопровождающие прохождение лавин, обеспечивали возникновение новых лавин. Это означает, что каждая лавина начинающаяся с одного электрона должна обеспечить возникновение хотя бы одного вторичного электрона, дающего начало новой лавине.

Если коэффициент γ дает число электронов выбиваемых из катода одним положительным ионом, то величина γ[exp(αd)-1], где d — межэлектродное расстояние, обозначает число вторичных электронов образовавшихся в результате прохождения единичной первичной лавины. Так как первичная лавина началась с одного электрона, то для воспроизводства лавин число вторичных электронов должно быть не меньше единицы. Таким образом условие самостоятельности разряда имеет вид

γ[exp(αd)-1] ≥ 1 (3)

Так как обычно exp(αd)>>1, то (3) можно упростить:

γ exp(αd) ≥ 1 или αd ≥ ln(1/γ)

Так как на катод приходят и выбивают вторичные электроны не только положительные ионы, но и возбужденные метастабильные молекулы и фотоны, то в (3) под γ понимаются все процессы образования вторичных электронов на катоде. В более общем случае вторичная ионизация должна учитывать и процессы в объеме газа, такие как, например, фотоионизация в объеме. Тогда уравнение (2) принимает более универсальную форму, применимую и в случае, когда процессы на катоде вообще не принимают участия в развитии разряда, как это имеет место в резко-неоднородных полях.

Искровой разряд. Закон Пашена.
При γ exp(αd) ≥ 1 ионизация, вызываемая последовательными лавинами, носит нарастающий характер, ток возрастает, что приводит к образованию искрового разряда, или искрового пробоя, при котором возникает тонкий проводящий канал, замыкающий промежуток. Напряжение, при котором для однородного поля выполняется условие (3), носит название пробивного напряжения. Так как и α/р, и γ зависят от напряженности поля Е/р, а напряженность определяется приложенным напряжением U и длиной разрядного промежутка d, то для однородного поля можно вывести уравнение зависимости пробивного напряжения от произведения р_d вида U_пр = f(pd), которое носит название закона Пашена.

U_пр = Bpd/ln[Apd/ln(1/γ)] (4)

где A и B — постоянные, характеризующие газ.

Эксперименты для разных газов дают хорошее совпадение с такой зависимостью.

В полном соответствии с этой формулой и экспериментальными данными получено простое уравнение для расчета пробивного напряжения в воздухе при давлении, близком атмосферному

U_пр = 24,5pd + 6,4(pd)^1/2 (5)

где р — давление газа, атм; d — расстояние между электродами, см; U — в кВ.

Зависимость для воздуха, соответствующая (4) и (5) приведена на рисунке ниже.

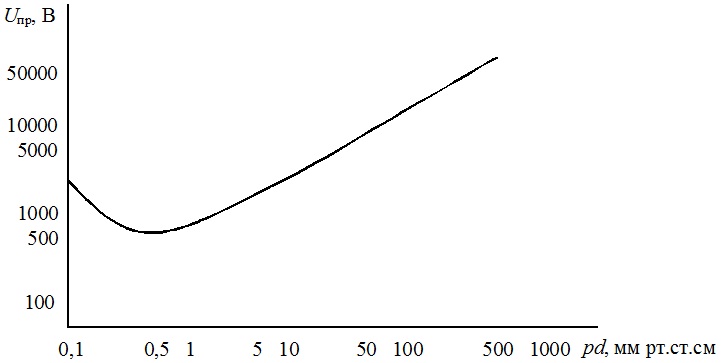
Зависимость пробивного напряжения в воздухе в однородном поле от произведения pd (закон Пашена)

При большой мощности источника напряжения, по каналу искры начинает протекать большой ток, что приводит к разогреву канала и возникновению в нем термической ионизации. Сопротивление канала резко падает, ток еще более возрастает, и возникает дуговой разряд, при котором ток может превышать сотни ампер.

Комментарии запрещены.