Индукционная зарядка частиц
Механизм индукционной зарядки поясним, рассматривая движение сферической проводящей частицы в поле плоского конденсатора (рис. 1)
Рис. 1. Схема индукционной зарядки частиц
Частица, попадающая в промежуток между пластинами, поляризуется (позиция 1). При контакте с электродом (позиция 2) взаимодействие зарядов частицы и электрода приводит к нейтрализации ближайшего к точке контакта поляризационного заряда. Далее, если частица отрывается (позиция 3), то она уносит избыточный заряд.
Таким образом, индукционный механизм зарядки включает поляризацию частицы в электрическом поле и нейтрализацию одного из зарядов. Не обязательно это происходит при контакте с электродом. Например, разделение зарядов происходит при разрыве капель в электрическом поле.
Зарядка при контакте с электродом в электрическом поле
Для расчета индукционной зарядки рассмотрим частицу в виде проводящего полуэллипсоида, находящегося на поверхности плоского электрода в электрическом поле (рис. 2), ε1 → ∞, удельные электропроводности γv1 = γv2 = 0).
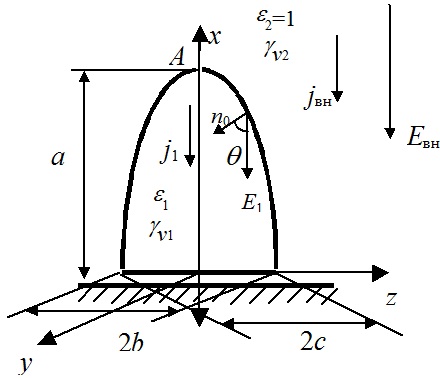
Рис. 2. Полуэллипсоид на электроде
Полуэллипсоид за счет изменения соотношения осей позволяет моделировать частицы различной формы. Форма в виде полуэллипсоида удобна для расчета поля, так как за счет зеркального отображения плоской поверхности электрода от системы полуэллипсоид на плоскости в однородном поле можно перейти к системе эллипсоид в однородном поле. Для такого случая известно аналитическое распределение поля на поверхности и в окрестности эллипсоида, находящегося в однородном поле.
Тогда напряженность электрического поля у поверхности проводящего полуэллипсоида Еn запишется в виде:
En = — [Eвнx]/[a2da][(x/a2)2 + (y/b2)2 + (z/c2)2]-0.5 (1)
где a, b, c — полуоси эллипсоида, da — коэффициент деполяризацции эллипсоида в направлении оси x.
Коэффициент деполяризации отражает изменение напряженности поля эллипсоидом в направлении соответствующей оси. Для сферы имеем da = db = dc = 1/3. Если сфера моделируется полуэллипсоидом, то b/a = c/a = 0,5 и da = 0,172.
Имея в виду, что плотность поверхностного заряда связана с напряженностью поля у поверхности электрода соотношением
σ = — ε0En (2)
то индукционный заряд полуэллипсоида можно определить по формуле:
q = ∫σds = — ε∫0Ends (3)
После подстановки (1) в (3) и интегрирования в эллипсоидальной системе координат по внешней поверхности полуэллипсоида получим:
q = — πε0Eвнbc/da (4)
Таким образом, проводящая частица на поверхности электрода в электрическом поле, вектор напряженности которого направлен к поверхности электрода, приобретает отрицательный заряд и на нее действует отрывающая от поверхности электрическая сила.
Зарядка полупроводящей частицы, находящейся на электроде в поле униполярного коронного разряда.
В общем случае частица характеризуется некоторой определенной величиной удельной объемной электропроводности γv1 и находится на электроде не в электростатическом поле, а в поле униполярного коронного разряда, т.е. γv2 ≠ 0 и Jвн ≠ 0. Тогда зарядка не проходит мгновенно и изменение заряда во времени определяется уравнением неразрывности плотности полного тока (тока проводимости и смещения) на поверхности частицы (рис. 2):
γv2E2n + ε0ε2 dE2n/dt = γv1E1n + ε0ε2 dE1n/dt (5)
Поскольку в начальный момент времени частица поляризуется как диэлектрический эллипсоид, то поле внутри частицы является однородным и направлено параллельно Евн. Это означает, что Е1n~cosθ, где θ — угол между нормалью к поверхности и вектором Е1. Отсюда из условия равенства нормальных составляющих вектора электрического смещения внутри и снаружи полуэллипсоида получаем:
E2n = E1n ε1/ε2 ~ cosθ,
где Евн — нормальная составляющая напряженности электрического поля на внешней поверхности полуэллипсоида.
Тогда плотность связанных зарядов σсвяз = ε0(E1n — Е2n) ~ cosθ.
Количество заряда, оседающего в единицу времени на единицу поверхности частицы в результате протекания тока коронного разряда равно:
J2n — J1n = γv2E2n — γv1E1n ~ cosθ.
Таким образом, суммарная плотность свободного и связанного зарядов σ = σА cosθ (пропорциональна cosθ), где σА — суммарная плотность свободного и связанного зарядов в вершине А полуэллипсоида.
Поскольку в процессе зарядки Е1n, E2n, σ остаются пропорциональными cosθ, то уравнение неразрывности (5) достаточно решить только для вершины эллипсоида А.
Для вершины эллипсоида справедливо:
E1nA = Eвн + daσА/ε0; E2nA = Eвн — (1 — da)σА/ε0 (6)
Подставляя (6) в (5) и интегрируя по поверхности частицы, получим:
q (t) = q∞ (1 — e-t/τ) (7)
q∞ = πε0bcEвн (ε1γv2 — γv1) / [γv1da — γv2(1-da)]
τ = ε0[ε0da + 1 — da]/[γv1da + γv2(1-da)]
где q∞ — предельный заряд, приобретаемый частицей, τ — постоянная времени зарядки частицы.
Из полученных зависимостей следует, что зарядка частицы во времени носит экспоненциальный характер.
При ε1γv2 > γv1 (частица плохо проводящая) q∞ > 0, т.е. частица приобретает избыточный положительный заряд и на нее действует прижимающая электрическая сила.
При ε1γv2 < γv1 (частица хорошо проводящая) q∞< 0, т.е. частица приобретает избыточный отрицательный заряд и на нее действует отрывающая электрическая сила.
Статическая электризация
Статическая электризация происходит при контакте и после-дующем разделении тел, обладающих различными физическими или химическими свойствами. Контактирующие тела приобретают заряды различных знаков. Статическая электризация происходит и в отсутствии внешнего поля. Основной физической величиной, определяющей электрические явления при контакте твердых тел, является работа выхода электрона. Разница работ выхода электрона у контактирующих тел проводит к нарушению их нейтрального состояния. Материал, для которого работа выхода Авых меньше, при контакте более легко теряет электроны и, таким образом, заряжается положительно. Значение образующихся зарядов пропорционально разнице работ выхода.
Для большинства диэлектрических частиц действует правило Коэна: при приведении в контакт и разъединении двух диэлектриков вещество с большей относительной диэлектрической проницаемостью заряжается положительно.
Так как состояние поверхности контактирующих частиц зависит от множества факторов (параметров внешней среды, загрязненности поверхности и т.д.), то приобретаемые заряды зависят существенно от конкретных условий и определяются экспериментально.